Posts
-
Primes, Riemann Zeta, and Pi, Oh My!
CommentsI’ve been working on other posts, but they’ve been harder to write than expected. A quick recreational math post should help fill the gap.
I’m targeting this towards the high school math contest audience. That means I won’t assume anything past calculus, but I will assume many things up to calculus, and I also assume people reading this will look up unfamiliar terms on their own.
Relatively Prime Random Numbers
Let \(a\) and \(b\) be two uniformly random natural numbers. What is the probability \(a\) and \(b\) are relatively prime?
First off, this problem isn’t well formed. You can’t define a uniform distribution over the naturals, because such a distribution would break probability theory axioms. (See here if curious.) To make this formal, we should really be picking naturals \(a,b\) uniformly from \(1\) to \(N\), and ask what the probability converges to as \(N\) approaches \(\infty\).
Let \(P(n)\) be the probability that two uniformly random natural numbers from \(1\) to \(n\) (inclusive) are relatively prime. What is \(P(\infty) = \lim_{n\to\infty} P(n)\)?
This was first solved by Dirichlet in 1849. For this proof, I’m handwaving the limit and assuming that random natural numbers act according to intuition.
Two numbers \(a,b\) are relatively prime if they share no common factors. This is true if and only if for every prime \(p\), \(a\) and \(b\) are not both divisible by \(p\).
Since we pick uniformly at random, the probability \(p\) divides a random natural number is \(1/p\). The probabillity both numbers are divisible by \(p\) is \(1/p^2\), giving
\[P(\infty) = \left(1 - \frac{1}{2^2}\right) \left(1 - \frac{1}{3^2}\right) \left(1 - \frac{1}{5^2}\right)\cdots = \prod_{p\text{ prime}} \left(1 - \frac{1}{p^2}\right)\]Now, here’s where you apply a neat trick. Take the reciprocal of both sides.
\[\frac{1}{P(\infty)} = \frac{1}{1 - \frac{1}{2^2}}\cdot \frac{1}{1 - \frac{1}{3^2}}\cdot \frac{1}{1 - \frac{1}{5^2}}\cdots\]For each fraction, substitute the infinite series \(\frac{1}{1-r} = 1 + r + r^2 + \cdots\).
\[\frac{1}{P(\infty)} = \prod_{p\text{ prime}} \left( 1 + \frac{1}{p^2} + \frac{1}{p^4} + \frac{1}{p^6} + \cdots \right)\]I claim the right hand side is the same as
\[\sum_{n=1}^\infty \frac{1}{n^2}\]The argument follows from a clever factoring argument. Suppose we expanded out the product of the infinite series. We would get infinitely many terms, where each term is generated by choosing one term from every infinite series and multiplying them together. For example, take \(1/2^2\) from the \(p = 2\) series, \(1/3^2\) from the \(p = 3\) series, and \(1\) from the rest. The term obtained is
\[\frac{1}{2^2\cdot 3^2} = \frac{1}{6^2}\]Now, take \(1/2^4\) from the \(2\) series, \(1\) from the \(3\) series, \(1/5^2\) from the \(5\) series, and \(1\) from the rest. That gives
\[\frac{1}{2^4 \cdot 5^2} = \frac{1}{(2^2 \cdot 5)^2} = \frac{1}{20^2}\]We can pick terms such that they multiply to \(1/n^2\) for any \(n\). For every prime \(p_i\), find the largest power \(p_i^{k_i}\) that divides \(n\). (\(k_i\) could be \(0\).) Then, take \(1/p^{2k_i}\) from the \(p_i\) series. By prime factorization, the product is
\[\prod_{p\text{ prime}} \frac{1}{p^{2k_i}} = \frac{1}{\left(\prod_{p\text{ prime}} p^{k_i}\right)^2} = \frac{1}{n^2}\]Every natural number has a unique prime factorization, so every \(n\) is generated once and exactly once. Thus, the product expands to the sum of the reciprocal of the squares
\[\prod_{p\text{ prime}} \left( 1 + \frac{1}{p^2} + \frac{1}{p^4} + \frac{1}{p^6} + \cdots \right) = \sum_{n=1}^\infty \frac{1}{n^2}\](If you’re like me, you may want to spend a moment admiring this argument. It’s a contender for my favorite proof ever.)
The final expression is
\[\frac{1}{P(\infty)} = \sum_{n=1}^\infty \frac{1}{n^2}\]Substituting
\[\sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}\]gives that the probability is \(6/\pi^2 \approx 0.608\).
Riemann Zeta And More Handwaving
Now, unless you’ve seen it before, it should not be clear why
\[\sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}\]This was first proved by Euler in 1734. His proof was a bit sketchy, and it took another 7 years to make it rigorous. Nevertheless, I’m presenting the sketchy proof.
To prove this result, we’re going to start from something completely different: the Taylor series for \(\sin(x)\). For all \(x\),
\[\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots\]Divide through by \(x\) to get
\[\frac{\sin(x)}{x} = 1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \cdots\](If you don’t know what Taylor series are, take this on faith. I don’t want to do calculus.)
The idea Euler used was to treat \(\frac{\sin(x)}{x}\) as an infinite degree polynomial. Any polynomial \(p(x)\) with roots \(r_1,\ldots, r_n\) can be written as
\[p(x) = a(x-r_1)(x-r_2)\cdots(x-r_n)\]where \(a\) is some constant. For this proof, we’re using a different form. Divide each term by \(-r_i\) to get
\[p\left(x\right) = a'\left(1 - \frac{x}{r_1}\right)\left(1 - \frac{x}{r_2}\right)\cdots\left(1-\frac{x}{r_n}\right)\]where \(a'\) is some other constant. Assuming this works for functions with infinitely many roots, \(\frac{\sin(x)}{x} = 0\) at \(x = \pm \pi, \pm 2\pi, \pm 3\pi, \ldots\).
\[\frac{\sin(x)}{x} = a'\left(1-\frac{x}{\pi}\right)\left(1+\frac{x}{\pi}\right)\left(1-\frac{x}{2\pi}\right)\left(1+\frac{x}{2\pi}\right)\cdots\]Equate this with the Taylor series. To make the constant term match up, we must have \(a' = 1\). (Try converting to the \(a(x-r_1)(x-r_2)\cdots\) form and you’ll see why it’s sketchy to assume \(\sin\) acts like an infinite degree polynomial.)
Group up the terms for roots \(k\pi\) and \(-k\pi\) to get
\[\frac{\sin(x)}{x} = \left(1-\frac{x^2}{\pi^2}\right)\left(1-\frac{x^2}{4\pi^2}\right)\left(1-\frac{x^2}{9\pi^2}\right)\cdots\]Now, compare the coefficient of \(x^2\). To get an \(x^2\) term, we have to choose \(x^2/(n^2\pi^2)\) exactly once, and choose \(1\) from the rest. This gives
\[-\frac{1}{3!}x^2 = \sum_{n=1}^\infty -\frac{x^2}{n^2\pi^2}\]Which gives the final answer of
\[\sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}\]This sum of reciprocals is a special case of the Riemann zeta function, defined as
\[\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}\]It turns out that analyzing this function for complex \(s\) has deep connections to the primes. I can’t explain why because I don’t know analytic number theory, but if you consider that we started from relatively prime numbers and got to here, I don’t think a connection is too strange.
\(\pi\) By Prime Products
I’ll close with a fun identity that relates the prime numbers to \(\pi\). This identity was also discovered by Euler.
Every odd prime \(p\) is either \(1 \text{ mod } 4\) or \(3 \text{ mod } 4\). Take the negative reciprocal if it’s \(1 \text{ mod } 4\) and the positive reciprocal if it’s \(3 \text{ mod } 4\). Add \(1\), take the product over all odd primes, and you get the identity
\[\frac{4}{\pi} = \left(1+\frac{1}{3}\right)\left(1-\frac{1}{5}\right)\left(1+\frac{1}{7}\right)\left(1+\frac{1}{11}\right)\left(1 - \frac{1}{13}\right)\cdots\]The proof borrows from both previous sections. First, take the reciprocal.
\[\frac{1}{1+\frac{1}{3}}\cdot \frac{1}{1-\frac{1}{5}}\cdot \frac{1}{1+\frac{1}{7}}\cdot \frac{1}{1+\frac{1}{11}}\cdot \frac{1}{1-\frac{1}{13}}\cdots\]Replace each term with an infinite series
\[\prod_{p \equiv 1 \text{ mod }4} \left(1 +\frac{1}{p} + \frac{1}{p^2}+\cdots\right) \prod_{p \equiv 3 \text{ mod }4} \left(1 - \frac{1}{p} + \frac{1}{p^2}-\cdots\right)\]And again, expand out the infinite product. Ignoring the signs, this is exactly the same as the product for relatively prime random numbers, except without an infinite series for \(2\). When expanded, we’ll get exactly one term for every odd number.
(I love this factoring trick so much. It’s great, even if it’s difficult to apply on other problems.)
Now, consider the signs of those terms. Term \(1/n\) is positive if and only if \(n\) is the product of an even number of (not necessarily distinct) \(3\text{ mod } 4\) primes. If you multiply an even number of \(3\text{ mod }4\) primes, you get a number that’s \(1 \text{ mod } 4\). If you multiply an odd number of those primes, you’ll get a \(3 \text{ mod } 4\) number.
So, the sign is negative at every other odd number, giving an expansion of
\[1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots\]which - surprise - is Leibniz’s formula for \(\pi\). (It follows from the Taylor series for \(\arctan\) evaluated at \(1\).)
\[\frac{\pi}{4} = \frac{1}{1+\frac{1}{3}}\cdot \frac{1}{1-\frac{1}{5}}\cdot \frac{1}{1+\frac{1}{7}}\cdot \frac{1}{1+\frac{1}{11}}\cdot \frac{1}{1-\frac{1}{13}}\cdots\] \[\Rightarrow\] \[\frac{4}{\pi} = \left(1+\frac{1}{3}\right)\left(1-\frac{1}{5}\right)\left(1+\frac{1}{7}\right)\left(1+\frac{1}{11}\right)\left(1 - \frac{1}{13}\right)\cdots\]Oh My! That’s All, Folks!
That’s all I’ve got. See you next time, for something less mathy.
-
AlphaGo vs Lee Sedol: Post Match Commentaries
CommentsDuring the five game match between AlphaGo and Lee Sedol, I posted my thoughts after each game to Facebook. People seemed to like them, so I’m collecting them here for posterity.
These are almost entirely unedited. Editing will add in my unconscious bias from knowing the match outcome, and I want to preserve how I felt while the match was in progress.
Game 1
I’m reading reactions to AlphaGo winning the first game, seeing comments like “I missed my chance to bet on a 5-0 result”, “Go is dead, RIP”, “No wonder Stephen Hawking warned us about artificial intelligence”, etc. And my gut reaction is, “Come on, yes it’s amazing and historic that AlphaGo won, but it’s 1 game, you can’t extrapolate it to a 5-0, you can’t extrapolate this to expecting AGI in a few years, that’s still pretty far away, OMG IT’S NOT THE END TIMES YET STOP SAYING IT IS.”
Then, I realized I had become one of THOSE people. Someone who’s always exasperated at AI reporting because it’s usually overloaded with biological connotations and simplified down to the point of deception. Someone who keeps hyping down AI progress because lots of people react very extremely to headlines when the reality is more nuanced.
In short, I’m matching the AI researcher stereotype. Andrew Ng sums it up best: his extreme optimism about the long term potential of AI is tempered by a relentless short term pessimism about current limitations.
So this time, I’m holding back the pessimism and trying to focus on the long term. I do think about AI displacing jobs, about AGI, about value alignment and AI risk. They’re worth thinking about and talking about, even if they can lead to extreme predictions of the future that make me internally facepalm.
A Go robot beat a pro with no handicap for the first time ever. Even if AlphaGo loses the match 1-4, this is still a watershed moment. It’s our generation’s Kasparov vs Deep Blue, and that deserves all the hype it gets.
I’m rooting for AlphaGo all the way. If it wins, I don’t even know what game’s next. I was going to say Arimaa, but it turns out bots started beating humans last year, so that’s out. Turn based perfect information games could actually be proclaimed dead in a few days, and that’s very surprising.
But, they aren’t dead yet. Four more games to go.
AlphaGo 1-0 Lee Sedol
Game 2
AlphaGo won again. A 5-0 isn’t out of the question, and an overall win is likely - it’s hard to see a world where Lee adapts enough to win the next three straight. I don’t know anything about Go, but I can argue this for other reasons.
One thing mentioned as strange in the commentary was AlphaGo playing seemingly bad moves that gave up points. This ties back into how both Go and Chess AIs are designed.
A game AI maximizes its chance of victory at all costs. A game AI does not care about margins. It does not care about time used. Its one goal is to win the game. Everything else is meaningless.
When a game AI plays a move that gives up free points, there are two plausible hypotheses.
-
The game tree search did not discover the move decreased win percentage, and the AI truly misplayed. Let’s call this “I dun goofed”.
-
The game tree search discovered the move increased win percentage, despite losing some points. For example, playing that move forces a sequence of replies that reduces the overall uncertainty. Let’s call this “consolidation”.
If the AI wins in the end, you should be suspecting consolidation, especially if it does “mistakes” in the endgame. Game AIs are strongest in the endgame, don’t assume they’re suddenly messing up. (Editor’s note: someone later convinced me this isn’t true for all game AIs, but it is true for Monte Carlo Tree Search AIs like AlphaGo.)
In a comment thread on a Go enthusiast site, someone tried explaining this. “If AlphaGo sees a move that wins by 1 point 90% of the time, and a move that wins by 10 points 80% of the time, it will pick the former.”
But that argument misses the point: AlphaGo DOES NOT EVEN KNOW THE POINT MARGIN EXISTS. All it sees is “win, loss, draw”. IT ONLY SEES THE RESULT. First, win. There is no second goal.
AlphaGo doesn’t see “90% chance win by 1 point, 80% chance win by 10 points”. It sees “90% chance win, 80% chance win”. When you look at a game that way, of course you’ll pick the 90% win.
That’s not saying AlphaGo ignores points. AlphaGo cares about them, but only as far as they help for winning. The point margins are already baked into its win percentage estimates. “How can I lose, and what can I do to stop that?” Look for answer, play move, repeat relentlessly. Over and over, until the other player has no hope.
People do this too. We’re just a lot worse at it than computers are.
When we predict games, our predictions are fuzzy, and we know they are fuzzy. If our prediction is off by +/- 2, and the prediction is a 1 point victory, we’re not going to go for a close game. If a human has a large point lead, they can afford more mistakes. I suspect that’s the argument we use to argue for pursuing point leads. We want to give ourselves breathing room.
Game AIs don’t have this problem, because after all their computation they have an exact quantification of their uncertainty, and they will trust that computation, blindly and absolutely.
This all builds to the key reason I think an AlphaGo 5-0 could happen. In the endgame, many moves before the resignation, AlphaGo made a move that many commentators called a mistake. It gave up some free points. That’s not a mistake, it’s consolidation. If AlphaGo needed those points, it wouldn’t toss them away. But, it decided that losing those points for sure was better than the chance of losing even more if it fought over them. Here, win the battle! I’ve still got the war.
If a game AI is fighting tooth-and-nail to the end, that’s good news for you. If it starts playing loose? Be afraid. Be very afraid.
AlphaGo 2-0 Lee Sedol
Game 3
It’s nice to see that instead of falling into despair. Lee Sedol is trying every possible avenue to victory.
After the 2nd game, Lee Sedol reportedly used the 1 day break to pull an all-nighter with several other Go pros, to come up with strategies to use on the 3rd game. At this point, the series isn’t about seeing how strong AlphaGo is. It’s about fighting for humanity’s pride. (Or at least the Go community’s pride. I’m sure DeepMind is very proud of what they’ve accomplished.)
The awesome thing is that these pro players actually have a good understanding of how AlphaGo works. Using that knowledge, they came up with a few key ideas:
-
In one game, many pros felt Lee Sedol made a mistake by not pursuing a ko fight. AlphaGo was unproven at this aspect of the game, so they recommended Lee try one to see AlphaGo’s response.
-
Lee Sedol decided he needed to focus heavily on the early and midgame. As the game progresses, AlphaGo’s play gets better, because every MCTS rollout takes less time. If he didn’t get a lead early, he wasn’t going to win. Lee accordingly spent much more time in the early game to make sure he played it right.
-
AlphaGo tends to simplify the board when it has a lead. So, Lee Sedol tried to complicate the game when he could. He didn’t know if he had a comparative advantage in complicated board states, but he knew he definitely didn’t have one in simple states.
By my understanding, Lee implemented all three. He played aggressively and carefully in the midgame, but was fended off and was down too much time to try a large scale attack again. Many pros felt the game was resignable, but Lee kept going to test AlphaGo. In the endgame, he tried ko fights and complicating moves, but AlphaGo managed both, and he was eventually forced to resign.
Even though he ultimately failed, it was still a good attempt. These were all reasonable hypotheses, and although none led to victory, it’s still better than not knowing.
It’s fascinating to see how quickly the narrative has shifted from “Can AlphaGo win?” to “Can Lee win?” As awesome as AlphaGo is, I’d like to see Lee win at least 1 game, if only for the storyline. Lee Sedol, rising from despair, carrying the hopes of humanity, cheered on by Go pros around the world? That’s an anime, and it’s happening right now. I guess anime really is real.
(Undertale reference. Don’t worry about it.)
AlphaGo 3-0 Lee Sedol
(Also, someone made this edit to Hikaru no Go. Never read the source, but I still liked it.)
Game 4
Holy shit.
Yesterday, I said I’d like for Lee Sedol to win a game for the story.
I DIDN’T THINK IT WOULD ACTUALLY HAPPEN. What in the world? Is anime real after all?
I have to admit that I only caught the end of the game today, so here’s my reconstruction from the GoGameGuru comments. Once again, Lee Sedol spent time in the early and midgame for naught, as AlphaGo gained a strong lead. On move 78, Lee Sedol played a very strong move. Michael Redmond (English commentator) praised it. Gu Li (Chinese commentator) called it “God’s Move” once he saw it.
AlphaGo replied wrong on move 79, although it wasn’t an obvious mistake, and some pro commentators were considering AlphaGo’s reply. By move 87, AlphaGo realized its mistake, and that’s where things get weird. AlphaGo made a series of surprisingly awful moves, letting Lee take a huge lead. (Even I thought S11 was awful, and I’ve played ~10 games of Go total in my life.) AlphaGo managed to chip away the lead over the endgame, but Lee replied well (while stuck in overtime from move 90 to boot! Replying with 60s thinking time is very impressive.) Soon, there were no chances left. AlphaGo resigns, room bursts into applause.
Like I said: this is actually an anime. Lee’s back is against the wall. He’s struggling to stand. “I can’t give up! For the world, I must fight!” He sees a move, and stuns the “perfect player”, the one who’s never lost. Move after move builds into a crescendo, a hurricane force, and AlphaGo doesn’t know what to do.
I haven’t seen any sports animes, but I’m pretty sure this plot fits just fine.
Naturally, Lee’s win led to an interesting press conference. If you missed it, seeing journalists look for a reason Lee won was very amusing.
Q: “Yesterday, you tweeted that the distributed version of AlphaGo has about a 75% win rate against the single machine version, which was still quite strong. Did you use the single machine version for this match?”
(Translation: Did you dumb down the AI to make Lee Sedol feel better after losing 3-0?)
A: “We used the same distributed version as the previous games.”
(Translation: there is no conspiracy.)
Q: “There’s been discussion on an information asymmetry. AlphaGo got to see all of Lee Sedol’s past games, and Lee got to see none of AlphaGo’s. Having played 3 games against AlphaGo previously, I’d like to hear Lee’s thoughts on this.”
(Translation: Do you think AlphaGo’s past 3 wins were only because Lee Sedol was unfamiliar with AlphaGo’s play?)
Lee’s A: “I didn’t know people were discussing that. I don’t see it as important. I did learn about AlphaGo in the past 3 games, but looking back I can only blame myself for my losses.”
Demis’s (CEO of DeepMind) A: “AlphaGo was trained on millions of games. We did not specifically train AlphaGo with games against Lee Sedol, and even if it had thousands of his games, it would barely affect the overall algorithm.”
(Translation: there is no conspiracy theory, and here’s why that conspiracy theory wouldn’t even work.)
For his part, Lee has shown very good sportsmanship. He made an interesting comment: “Losing a game after winning three would have been devastating. Winning a game after losing three is exhilarating in its own way.” I have to agree. Suddenly, the stakes on game 5 look much higher. There’s hope for an almost even 3-2. (4-1 is still more likely.)
So, what went wrong for AlphaGo? I’ll explain the leading theories, then explain why they don’t actually matter.
The theory is that first, AlphaGo didn’t consider the line Lee Sedol played. It was too difficult to derive during the Monte Carlo Tree Search (MCTS), and Lee found a blind spot. Once AlphaGo realized its predicament, the mechanics of Monte Carlo search brought it into a downward spiral.
Recall that AlphaGo’s one objective is to maximize win percentage. If AlphaGo evaluates a board as losing, it means that AlphaGo thinks if it had to play itself from that board, it would lose more often. This makes the MCTS biased to extreme outcomes that could lead to a win if the opponent misplays. AlphaGo plays such a move, but the mistake is so obvious that the (human) opponent will never make it. The human replies correctly, and AlphaGo’s position deteriorates. “Well, I’m losing. But if I make this crazy move, and the other player messes up, I could still win.” Make crazy move, get sane reply. “Well, I’m losing. But if I make this crazy move, and the other player messes up, I could still win.” Make crazy move, another sane reply. Keep going, and going…
It’s a downward spiral that has claimed weaker MCTS-based Go AIs in the past. AlphaGo somehow got itself out of the spiral, but by then it was too late.
If a human were in AlphaGo’s position, they would model Lee Sedol as a strong player who would never make that mistake. They would instead play moves that limit the damage, and wait for an opportunity elsewhere.
But AlphaGo doesn’t model its opponent. It’s not worth it and it’s too difficult, which is why suggesting DeepMind trained AlphaGo specifically as a Lee Sedol killing machine is so laughable. AlphaGo is a human agnostic. The only opponent AlphaGo has for evaluating moves is itself.
Against an opponent of itself (the strongest player it knows), playing safe while losing wouldn’t increase win %. If an MCTS AI thinks the odds of opponent misplay are better than the odds of winning with safe play, it will put all the chips on that chance. I’ve actually seen this happen in my own research. While getting started, I ran MCTS on Tic-Tac-Toe to test my code. If you have two moves that both lead to a 3-in-a-row, MCTS will block neither 3-in-a-row. It’ll instead create a 2-in-a-row elsewhere, because its best chance is to hope it gets another turn. What happened today is the same principle, except on a larger timescale with more uncertainty.
Maybe playing safe would be the right play if AlphaGo knew it was playing Lee Sedol, but AlphaGo couldn’t know it was playing Lee Sedol.
Based on my experience, and on the testimony of pro players who have tried other Go AIs, and on the anecdotes relayed by people who have toyed with MCTS before, this is by far the explanation I trust the most.
And it’s all slightly missing the point.
These are theories, backed up by past experience and evidence, but they’ll never progress past guesswork. AlphaGo plays millions of random games a second. Its board evaluation is informed by a deep convolutional neural net, which is a legendarily difficult to interpret black box. To pick a move, AlphaGo runs millions of black box computations, averages them all, and gives a response. Why AlphaGo didn’t see Lee’s “Hand of God” play, why AlphaGo was so sure it needed a mistake to catch up, and whether AlphaGo was correct in that assessment or not is all incredibly difficult to explain, because its behavior is based on so much raw work. If DeepMind finds a concrete explanation for AlphaGo’s collapse this game, hats off to them, because I don’t think they can do it. I expect reasonable theories at best.
Almost all machine learning used today runs on black boxes. We show this image recognition model does 0.5% better on this dataset than the old one, but it’s usually not clear why, and very smart people have to try hard to justify why a machine learning method works over another. (Surprisingly often, the key to good performance is to throw everything at the dart board and see what sticks.)
For now, it’s fine. Computers are only good at maximizing exactly defined utility functions, and it’s on the human to describe a utility function that makes the AI do what we want. In the future. when computers are good at maximizing ill-defined utilities? Well, that’s when you get the paperclip optimizers people like to talk about when advocating for AI safety. I may not agree on the timetable for AGI, but I agree it’s worth doing work on now. (For what it’s worth: 75% confidence interval on 20-40 years, and I think AI risk research is around as funded as it should be right now. I donated $20 to MIRI last year since it sounded like they could use the help.) (Editor’s note: after some Facebook discussion, I’ve since revised this to 50% confidence for 30-55 years, with more weight towards the end of the range, and believe AI risk could use more funding.)
Today showed AIs can exhibit strange emergent behavior in the right circumstances, causing them to jump from “smart” to “insane” in a second. The first question from the press conference hit this nail on the head.
Q: “Today, we saw AlphaGo make many unfathomable mistakes to experts. They thought these moves made no sense, but were hesitant to question AlphaGo. They weren’t sure if AlphaGo’s mistakes were actually mistakes. If this happened in real world usage, like something medical, and it recommends what looks like a mistake to experts, and people don’t question it because they think there’s a bigger picture, it could lead to lots of confusion. So, I’m curious to hear your perspective on that.”
It was a great question that cut to the heart of the matter. DeepMind is already eyeing medicine (see DeepMind Health), so this is especially relevant.
Demis’s A: “You have to remember AlphaGo is a prototype. I wouldn’t call it a beta, or even an alpha. So of course, part of why we’re doing this match is to test our methods against skilled humans. We’re also playing a game, a beautiful game. Healthcare would be a different matter, and of course it would require stringent testing like other software. This is a prototype we’re testing, so I think it’s a different situation.”
It’s a good point with no easy answers. Trust the AI (who can crunch numbers and read orders of magnitude more data), or trust yourself (and the intuition gained from your comparatively little knowledge)? If something goes wrong, whose fault is it? Yours for trusting the AI too much, or yours for trusting the AI too little?
I’m optimistic we can figure these issues out. We had a small viewing party in the lab for Game 1, and a human-computer interaction professor made an interesting anecdote: humans lose to computers in chess, but a human with a computer partner beats other computers. The human isn’t dead meat despite being individually useless. They can still contribute something. It’s nice to know we’re not obsolete yet.
AlphaGo 3-1 Lee Sedol
(Michael Redmond’s reaction to move 78: YouTube video.)
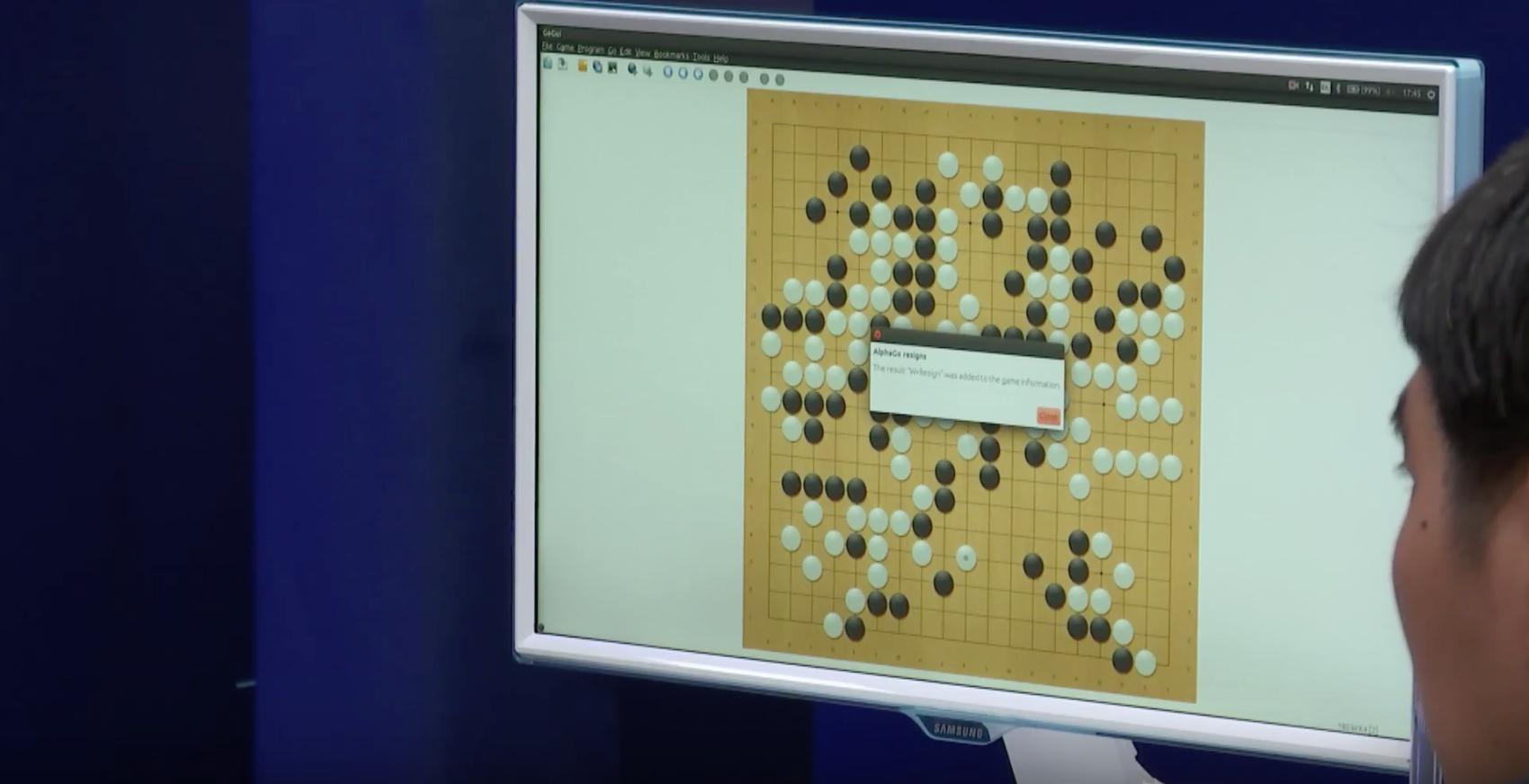
AlphaGo resigning. Click for larger version.
Game 5
Final match ends in a win for AlphaGo as expected.
The short summary of the game: in the early game, AlphaGo didn’t recognize a known tesuji, letting Lee Sedol gain a sizable lead in the bottom right. However, over the rest of the game AlphaGo was one step ahead of Lee Sedol (commentators said the key point was Lee losing in top-left) It was just enough to let AlphaGo make a comeback, and Lee resigned with the board almost filled to completion. (People say the board ends with AlphaGo winning by 2.5 points)
First off, I want to highlight how much Game 4 dominated the commentary. As soon as AlphaGo made a mistake, people asked if game 4 was going to happen again. Chris Garlock (English co-commentator) kept prompting Michael Redmond to indicate whether he thought AlphaGo’s moves were a sign of it blowing up or not. Of course, based on the match result they weren’t. In fact, it sounded like AlphaGo played almost every move well, and the only questionable moves were ones that appeared when AlphaGo was leading.
It’s really interesting to see how much people tried to read into AlphaGo’s evaluation of the board based on the moves it made. An aggressive move must mean it thinks it’s losing! A slack move must mean it thinks it’s ahead! Well, there’s certainly some correlation, but it’s definitely not that clear cut.
That’s a nice segway for the topic I decided to close on: anthropomorphization of AlphaGo. (Not going to lie, had to Google that to make sure I spelled it right.)
Everyone is very guilty of giving human qualities to AlphaGo, including me. People have described AlphaGo’s play as calm or collected or aggressive or smooth, as if AlphaGo is a person. Some commentators call AlphaGo a “she’. The Chinese stream started calling AlphaGo 阿老师, which translates to “Teacher Ah”, for “Teacher Alpha Go”. AlphaGo has even been given an honorary 9 professional dan rating from the Korean Baduk Association.
This isn’t limited to the commentators, the technical side has done this too. One of the onsite DeepMind engineers did an interview during the game about what it’s like in AlphaGo’s control room. He described it as monitoring the heart of AlphaGo, making sure communication to the datacenter is working, verifying failing machines are automatically rebooted, and so on. (Yes, it is run over the network. I believe it’s connected from a datacenter in the central US.) During game 4, Demis made a tweet saying AlphaGo thought it was doing well before realizing its mistake. He then had to clarify that “thought” and “realization” meant “AlphaGo’s estimated win % was high, then dropped.” In these very writeups, I’ve said things like “AlphaGo thinks”, when the more accurate thing to say is “AlphaGo runs millions of simulations.”
On one hand, I don’t think anthropomorphizing AI is a bad thing. Many of the algorithms in AI are motivated by real life biology. It’s much easier to explain AlphaGo using human analogy. At some point, trying to pedantically explain exactly what AlphaGo is doing every single time is just going to get tiring. There’s a concept called the duck test: if it looks like a duck, swims like a duck, and quacks like a duck, then it probably is a duck. If AlphaGo plays like a human, if its algorithms share similarities to a human’s, if it can beat a professional player like a human, then maybe it’s okay to treat it as a human.
But, the reason it’s important to be careful about humanizing AI too much is that many people assign human qualities to AI far more easily than they should, and it makes people both overestimate and misunderstand how AI works. AlphaGo does not think, if by think you mean how a human thinks. It does not have a heart, if by heart you mean something like a human heart. When we say “think” or “heart”, we really mean “a very rough approximation to human thought” and “a very rough approximation to a heart”. The problem happens when people think “think” actually means “think like a human” when it doesn’t. It really, really, does not. Is it any wonder that Yann LeCun got pissed off when he read someone claim that strong AI didn’t need any more breakthroughs?
Anthropomorphizing AI makes it sound like we know a lot more than we actually do, and suggests strong AI will think like humans do, and both are dead wrong. And that’s why I get annoyed at it, even as I use human analogies in my own speech.
Looking back, that’s why I started doing these write-ups in the first place. It let me explain just how far these analogies apply, meaning not very far at all.
And this is just for a MCTS-based game AI. This is by far the area I’m most qualified to talk about. I know I’m still missing a lot of the bigger picture, and some of the comments made on day 1 were still incredibly exasperating to read.
It’s given me some food for thought. If I can tell AI discussion is simplified so often, I should recognize that most of my knowledge must also be founded on very heavy abstraction that hides the underlying complexity, and that if I state it too confidently it’ll probably piss off other people as well.
To paraphrase a source I can’t remember:
The thing I hate about those 800-page high school textbooks is that they suggest we’ve solved biology, chemistry, and physics. We haven’t even scratched the surface. I’m worried they’ll make students think there’s nothing more to discover. That all the answers are written down. One book for Everything About Insects. One for Everything About Light. One for Everything About Algebra. I’m worried students won’t understand what it means to be a researcher.
AlphaGo vs Lee Sedol was the highest profile experiment of AI to date, and even if you were supporting Lee Sedol and were crushed when he lost the first 3 games, I think this match is still worthy of applause, if only because it was a real-world test of the capabilities of AI. It’s been exciting. Can’t wait to see what’s next.
AlphaGo 4-1 Lee Sedol
(Oh god, I’m typing this during the final press conference and a reporter just asked how many clones of AlphaGo DeepMind has and how many they were planning to make. I do not have enough hands for the amount of facepalm I want to do.)
(Woops, and another reporter is suggesting DeepMind hosted this contest to see the public’s perception towards AI, and wanted to know how DeepMind’s ethics board will handle the people’s fears about AI. I mean, sure, it could be part of their reasoning, but it’s definitely not their main reason for hosting the match.) (Editor’s note: and connoting that DeepMind had a motive so vaguely sinister isn’t doing me any favors.)
-
-
Lessons Learned After Six Months of Blogging
CommentsJust over six months ago, I rebooted my personal site and started blogging. So far, I’ve been pleasantly surprised at the response. It’s encouraging to know people like reading my own brand of stupidity.
As celebration, I decided to reflect on the lessons I’ve learned. The part of me that loves all things meta wouldn’t forgive myself if I skipped a chance to write a blog post about my blog.
***
1. Just Write. It’ll Get Better
Of my four most recent posts, not counting this one, three are among my favorites. That’s not a coincidence.
If you’re worried you can’t write well, write anyways. Everybody cringes when they read their past writing, me included. It’s all part of the process.
The ceramics teacher announced on opening day that he was dividing the class into two groups. All those on the left side of the studio, he said, would be graded solely on the quantity of work they produced, all those on the right solely on its quality. His procedure was simple: on the final day of class he would bring in his bathroom scales and weigh the work of the “quantity” group: fifty pounds of pots rated an “A”, forty pounds a “B”, and so on. Those being graded on “quality”, however, needed to produce only one pot — albeit a perfect one — to get an “A”. Well, came grading time and a curious fact emerged: the works of highest quality were all produced by the group being graded for quantity. It seems that while the “quantity” group was busily churning out piles of work-and learning from their mistakes — the “quality” group had sat theorizing about perfection, and in the end had little more to show for their efforts than grandiose theories and a pile of dead clay.”
(David Bayles, Art & Fear)
Or said more succinctly,
Sucking at something is the first step to becoming sorta good at something.
(Jake The Dog, Adventure Time)
2. Your Writing Environment Matters. Take The Time To Find One That Works For You
My old site ran on Blogger. It worked, but I quickly lost motivation to update it. Blogger abstracts its functionality behind lots of tools, and I got sick of it. To create posts, I had to open Blogger’s site and write in their Microsoft Word-esque editor. To change the site layout, I could either use a drag and drop interface, or edit raw HTML. Plus, the Google+ tie-in was vaguely annoying.
In contrast, Github Pages has been a complete joy. It’s transparent, I have total control over my site’s design, and best of all I get free edit history thanks to Git. I know it’s incredibly nerdy to say this, but getting to write my blog posts in Markdown using Vim is fantastic.
So far, my blog uses images, audio clips, code highlighting, Youtube embeds, spoiler buttons, typeset math (from KaTeX), comments (from Disqus), and analytics (from Google Analytics). Not only does it all work, I know how it all works, which is a huge plus.
If you’re familiar with Git, it’s surprising how natural blogging in it feels. I can switch between different drafts on a whim, and can move from coding to blogging with ease if I need to take a break from debugging. The only issue I’ve had so far is a conflict between KaTeX and the Markdown rendering engine, but even that wasn’t so bad. After figuring out the problem, I added a hotfix the same day.
If you don’t like your writing environment, you aren’t going to write. There are lots of obstacles between having an idea and writing about it. Your environment shouldn’t be one of them.
3. It’ll Take Longer Than You Think. No, Longer Than That
I never planned to have an update schedule. As a student, I knew my work loads could shoot up in an instant, and I didn’t want to feel obligated to write something when I didn’t have the time to do it properly.
What I didn’t expect was how long writing would take. Without fail, every post I write takes longer to finish than I think it will. This is even after I try accounting for the planning fallacy. As said by Douglas Hofstadter,
Hofstadter’s Law: It always takes longer than you expect, even when you take into account Hofstadter’s Law.
(from Gödel, Escher, Bach)
Proving Hofstadter’s Law wouldn’t be so bad if I didn’t do most of my writing at midnight. To show why it’s awful, here are the commits for my first technical post.
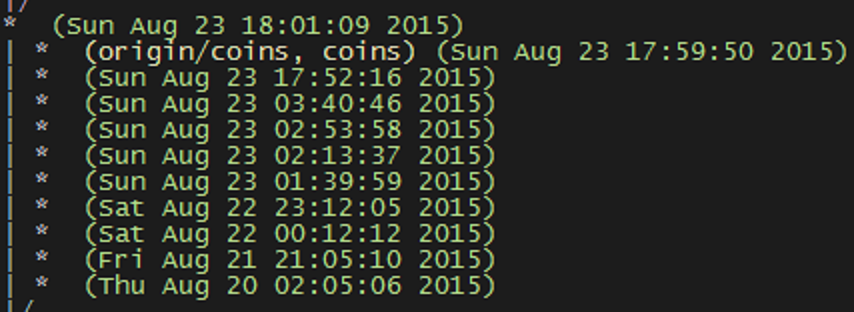
Pictured: my slow descent into madness
- Initial work saved Thursday, 2 AM
- Completed a first draft Friday night, working from 9 PM to midnight.
- Started revising Saturday night. Started at 11 PM, hoped to finish by 2 AM. Still working at 3:40 AM.
- Final launch at Sunday 6 PM. Attempted to fix my sleep schedule for Monday, failed miserably.
I have literally lost sleep to blogging. It’s silly, it’s stupid, and I don’t see it changing anytime soon. In fact, I’m doing some late night writing right now. Check the commits for this post. You should find a commit at 1 AM, another at 2 AM, a few 3 AM commits mixed in…

Pictured: my descent into madness, complete
It’s okay to get frustrated at your writing speed. Everyone wishes they could write it well the first time, but no one does. Try not to let it bother you, and keep going. I find that taking my rage out in commit messages helps.
More things. All the things. man whose going to read these commits anyways (Sat Dec 19 03:36:46 2015)
Time to in medias res this shit up (Sat Dec 26 16:50:37 2015)
Too lazy to make good commit message (Sun Jan 3 18:28:00 2016)
URGH JUST SHIP IT. (Sun Jan 10 11:50:03 2016)
Incidentally, this is why you should consider a CFAR workshop. Reading about logical fallacies doesn’t actually stop you from making them. I haven’t done one because the cost is scary, but I’ve considered it.
4. Don’t Worry About Your Ideas. Worry About Your Time
In the past 6 months, I’ve written fourteen posts. Fifteen, if you count this one. That averages to just over one post every 2 weeks.
I have blog-worthy ideas more often than once every 2 weeks. When I started this, I was worried I’d run out of things to say, but the opposite has turned true; I have too many ideas, and need to filter them aggressively.
I consider myself a slow person in all aspects of life. I rarely solve a problem at first glance, unless I’ve seen a problem that’s very very similar. I almost never ask questions in lecture, because I’m usually so lost I can’t articulate what I’m confused about. And when it comes to writing, I have to phrase an idea once in the head and thrice on the page before I’m satisfied.
Being slow isn’t bad, but it baffles me that web serials like Worm and blogs like Slate Star Codex can update over once a week. I certainly can’t do that. It requires a level of discipline I don’t have yet.
I think people undervalue how impressive sticking to a schedule is. We’d all be a lot better off if we valorized organization more.
5. Your Writing Style Is Your Speaking Style. Embrace It
When I started this blog, I chose to keep it colloquial. It’s my blog, and it’s my voice. If I want to use contractions or swear a bit, I will, formal writing conventions be damned. If my posts drag on, that’s part of who I am, I won’t hide it.
I don’t want to feel obligated to write a certain way, or present only certain parts about myself. I write things I’ll want to read later. If other people read them too, that’s cool.
Once I started writing like how I’d talk if I had the time to phrase things just right, I started noticing patterns. I start sentences with “and” or “but” or “because”, since I like the abruptness of the conjunction. I say “A and B and C” instead of “A, B, and C”, because sometimes I don’t like the mental pauses from the commas.
I use sudden paragraph breaks to emphasize specific sentences. I insert parallel structure to connect disparate ideas.
Parts of this are just for good style, but style isn’t a list of conventions you have to follow. It’s how you say the things you want to say.
When you write, you’re trying to say something. So actually say it. Don’t couch it in formal writing. If that means you add Internet memes everywhere, then so be it.
There’s a time and place for formal writing. Blog posts are neither the time nor the place.
6. Do Peer Review Whenever You Can
I usually don’t ask friends to read my posts before I share them. I want to work on my revision skills, and it feels cheap to outsource it to other people.
However, sometimes I decide I want more polish. I’ve asked for feedback on three posts: The Other Two Envelope Problem, “How Do You Feel About Grad School?”, and A Gentle Introduction to Secure Computation
Every post improved by an order of magnitude.
It’s hard to describe how much peer review helps. After reading so many drafts, your brain starts blurring the words together. You miss the forest for the trees, and getting another reader helps immensely with untangling this.
Even the best writers send drafts to editors and friends. There’s no shame in it. What’s more surprising is how little I valued it before now. It took me until my secure computation post to begin appreciating it, and I think I still don’t value it enough.
7. Effort Doesn’t Drive Quality, Experience Does
This one surprised me. Consider two posts, one about Doctor Whooves Adventures, and the other about AlphaGo.
The first was very difficult for me to write. I didn’t know why I liked Doctor Whooves Adventures, and even after that post I find it hard to explain why I hope the series isn’t dead. Over two weeks, I agonized on how to express my love for the show. I went back and forth between different excerpts and ideas, and eventually posted a final draft to a lukewarm response. Looking back, I can see why.
In comparison, the post on AlphaGo was written in a single night. I wanted to strike while the iron was hot, since I knew interest in Go would be fleeting. Thanks to prior experience with the research areas involved, I got the gist of the paper in a single read, and thanks to thinking about these topics for over a year, I was able to quickly articulate my feelings on the result.
On review, my strongest posts are almost all technical. It’s what I have the most experience writing. I’ve been writing proofs since high school, gave a math talk in 11th grade, and did two research presentations last semester. Of course my technical posts are going to be better than my non-technical posts, I’ve had years of practice for the former.
That’s not saying all my non-technical writing is bad. My best post is still my non-technical think piece about grad school. What I’m saying is that if you’re going to write about something unfamiliar, don’t be surprised if it takes you ages to churn out something mediocre. The first draft of my graduate school post was awful, and it took a month of revising over winter break to get it to that state.
8. Try Not To Get Hung Up On Popularity
We all want other people to care about us, even when we give ourselves reasons why they shouldn’t. Writing is no exception. In fact, it’s an extra dangerous area. When you share a personal story or spend hours thinking about the easiest way to explain something, you can’t help but grow attached to your work. It’s like a little baby, and watching your baby get ignored is like a punch to the gut.
It’s obvious, but it bears repeating: popular things are not always good, and good things are not always popular. I’m a bit obsessed with checking my blog views, more than is healthy, and I need to remember to divorce my feelings about a post from its view count.
What people think about your work matters. But don’t let it rule everything about you. According to Google Analytics, my three most viewed posts are:
- A Gentle Introduction to Secure Computation
- “How Do You Feel About Grad School?”
- Mystery Hunt 2016 Wrap-Up
The first stuck on Hacker News for a day, and the last got shared to the Mystery Hunt subreddit. Note that both reasons for the high view count are only tangentially related to the actual quality.
If I cared only about view count, I wouldn’t bother writing about a My Little Pony made-for-TV movie, because I know most people won’t be interested. But I care about it, and that’s why I did it.
(For the record, both my AlphaGo post and my Khan Academy post deserve more views than they have. You really shouldn’t read that MLP post unless you’re interested in me commentating a nerd-snipe.)
***
We’ll see how I feel about these lessons in the future. If there’s one constant in the universe, it’s that everyone thinks their past self is an idiot.
As for the next few months? I plan to start flushing my queue of non-technical post ideas. On the short list are
- A post about Gunnerkrigg Court
- A post on effort icebergs and criticism
- A post about obsessive fandoms
- A post detailing the hilariously incompetent history of the Dominion Online implementation
I may also try writing some short stories. I haven’t done creative writing since high school, but after reading so much web fiction, I’m up for giving it a shot.
At my current rate, four posts will take two months. With planning fallacy, maybe three. Knowing that I still overshoot my estimates…six months? Hopefully I can do more than that though.
I’ll close with a quote, something as “me” as I can find.
SP: Do you see now, Doctor? This land is divided, and there is no fixing it.
Doctor: Oh, I do see…I see that this cannot stand. I see that things are wrong here. Things are very, very wrong, and I don’t like it very much. I see that there is pain here, and I don’t like that either. I see that you’ve grown complacent. I think everyone has. There is nothing worse for life than complacency, and I shall not have it. I might not know many things about this land of myth and magic, but I know that Twilight is on the other side of this conflict and I know that this conflict is causing misery. I’m going to correct both those things.
(Doctor Whooves Adventures, “Bells of Fate”)
Keep going. Keep trying. Because whether it works out or not, it’s sadder to not try at all.
Onwards and upwards!