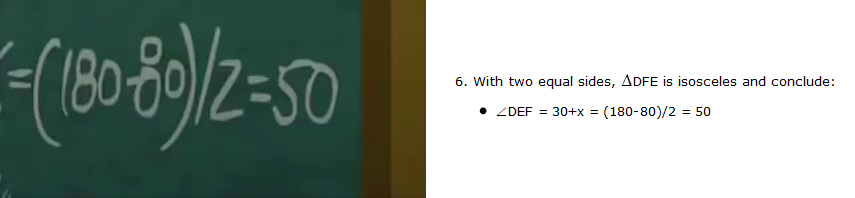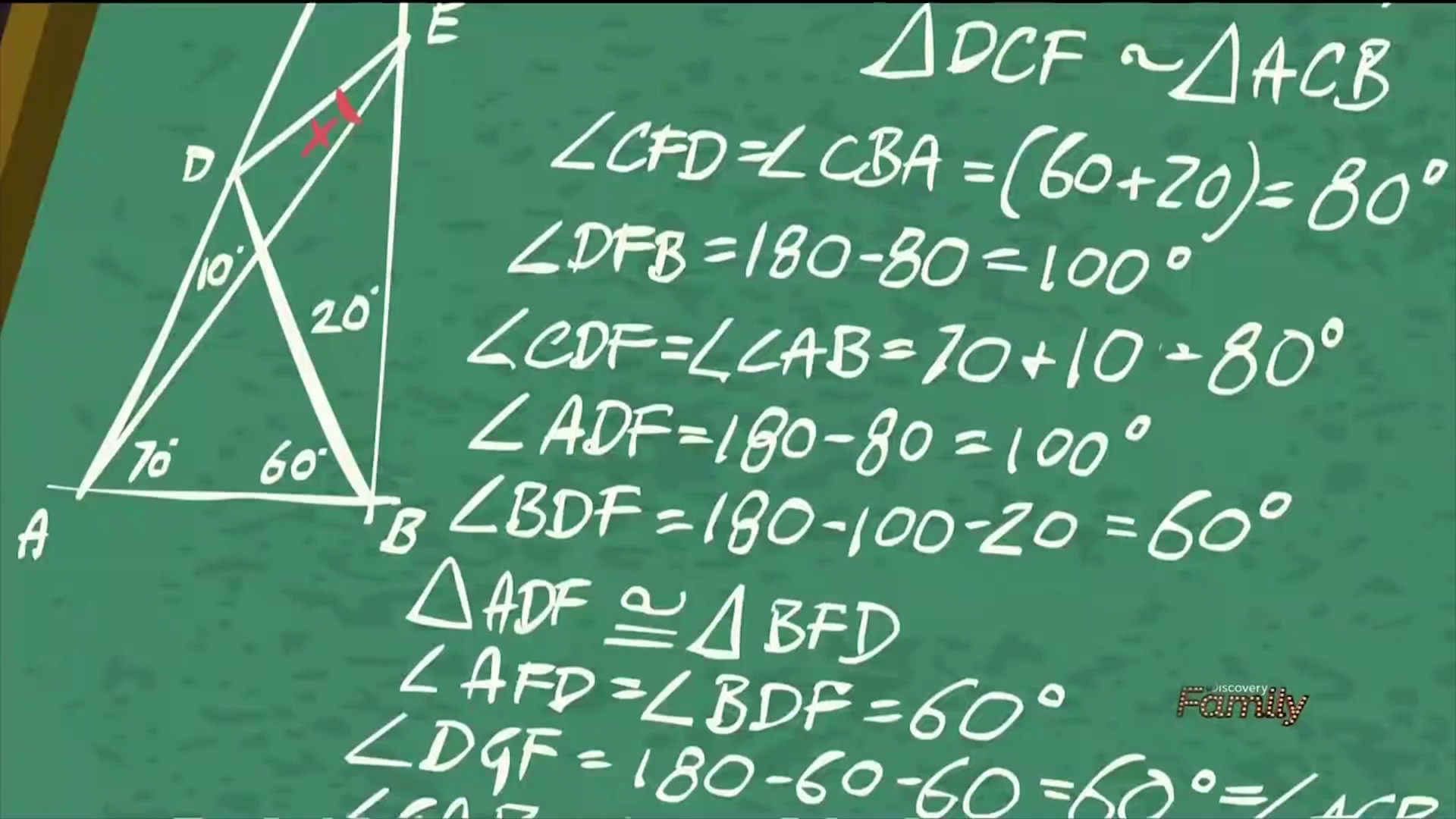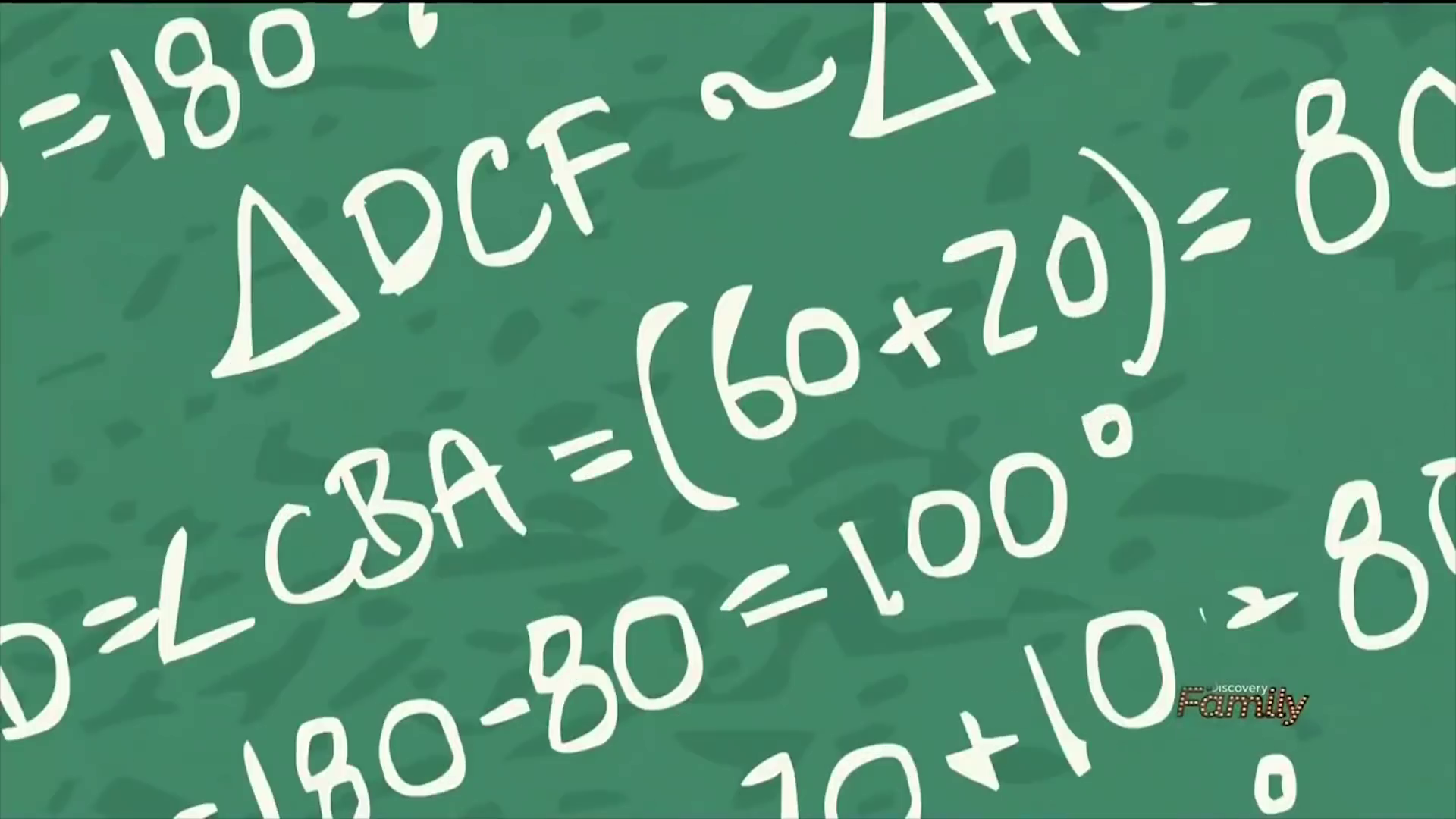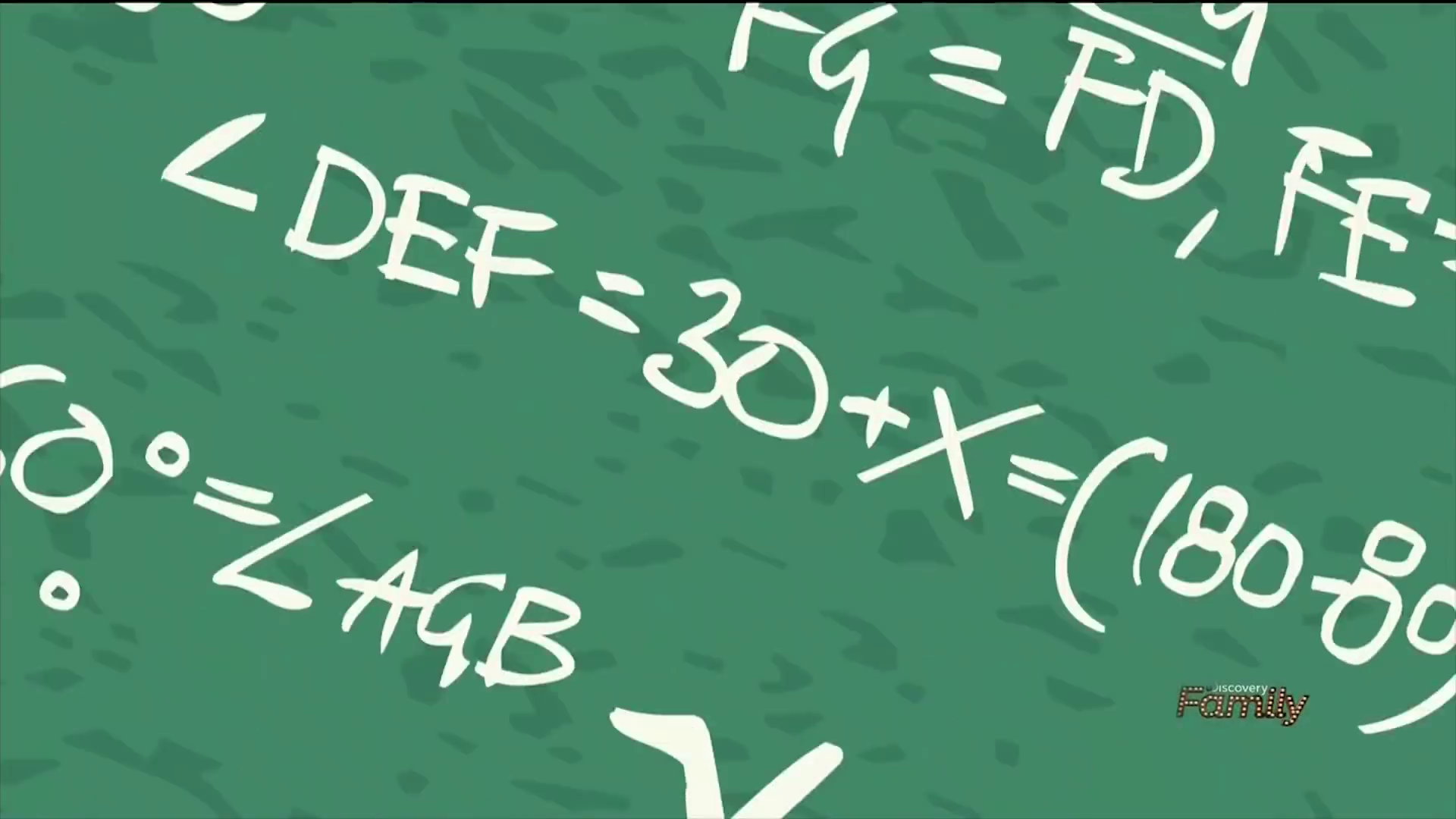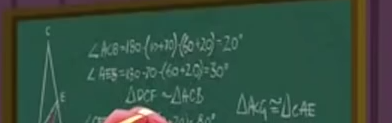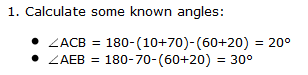Math in Movies: The Friendship Games Geometry Problem
(Very minor spoilers for Friendship Games. Read at your own risk.)
(Click on any image to see the full size photo.)
It’s not well known outside the fandom, but My Little Pony: Friendship is Magic has a high school spinoff called Equestria Girls. It’s a movie series that exists only because of the merchandise potential. Reception to the films is mixed, but it’s widely agreed they’re nowhere near as good as the show.
The most recent entry, Friendship Games, came out September of this year. It’s…well, it’s definitely a movie. The pacing is off, the plot is silly, and the world stretches suspension of disbelief way too much. (Magic is real, humans are growing wings, there’s a portal to an alternate universe, and no one outside the school knows about it despite almost no attempts to hide it. Really?)
That being said, I still enjoyed it. The animation is excellent, and the songs are catchy. Here’s one of those songs.
[Sunset Shimmer and Wondercolts] Ho! We're gonna take you down Ho! We're gonna take you down! Take you down! (Ho! We're gonna take you down!) Take you down! (Down, down, down) [Shadowbolts] (Oh oh!) We're here to take you out (Aw aw!) We're here to take you out (Aw aw!) Take you out! (We're here take you out!) Take you out! [Wondercolts] We're not about to let you win So get out of our way Think you got us beat But we're here to stay United strong, yeah, we'll take you down You're not so tough, now you're in our town All of the times we lost before Not about to give up, we're only bringin' in more We can smell your fear, we can see your sweat Hope you didn't spend money 'cause you're losin' this bet! You've got nothin' on us Na, na, na-na-na, na Let's go, Wondercolts! You've got nothin' on us Na, na, na-na-na, na Let's go, Wondercolts! [Shadowbolts] Talk a little too much for a school that never wins Maybe you should just stop 'fore you even begin We are Crystal Prep High and we have a reputation Every little moment is about our education Put your ear to the ground Listen to that sound You're a house of cards And it's about to fall down (fall down) About to fall down (fall down), hit the ground You've got nothin' on us Na, na, na-na-na, na Let's go, Shadowbolts! You've got nothin' on us Na, na, na-na-na, na Let's go, Shadowbolts! [Wondercolts] Pressure's on Now we're gonna beat you Step aside, it's time that we defeat you Crystal Prep yourself 'cause you're about to go Down, down, down, down [Shadowbolts] Pressure's on You know we're gonna take you Just give up before we have to break you Canter-not-a-lot, you're about to go Down, down, down, down [Wondercolts] Take it up to the top 'Cause we know we can win [Shadowbolts] Maybe you should just stop 'Cause we've seen you give in [Wondercolts] We believe in ourselves And we've got what it takes [All] And we're not gonna stop [Sci-Twi] I can't wait 'til this is all over There's so much more that's going on [Sunset Shimmer] And before these games are over I'll find out just what she's done [All] Can she do it? Will she make it? Who will win it? Who will take it? Can she do it? Will she make it? Did she win it? Did she make it? Who's the winner? Who's the reject? How did she answer? Principal Cinch: Incorrect!
This segment is a ton of fun. It gets so much mileage out of facial expressions and body language, the way good animation should. I’d also like to point out all the badass science and carpentry these girls are doing. Hooray for casually breaking gender stereotypes!
But, that’s not what this blog post is about. It’s about this frame.
Wait. Is that…
It is.
It’s Euclidean geometry.
Let me explain why this is the best thing ever.
I did math contests in high school. My favorite subject was Euclidean geometry. I took a course on Euclidean geometry for math contests. I made honorable mention in Bay Area Math Olympiad because I knew about radical axes. This is an animation of two high school students competing on a geometry problem. THIS WAS ACTUALLY MY LIFE. One huge part of my identity got animated into another huge part of my identity. It’s so wonderful.
And the animators didn’t half-ass it either. These chalkboards look like valid geometry proofs. There’s no immediate reason to believe they aren’t. I wonder if the proof’s correct…
Cue the nerdsniping.
***
To investigate this, I first gave the animators the benefit of the doubt and assumed it was real. There’s a good reason to assign a high prior on this. The time travel episode from season 2 of Friendship is Magic included equations from special relativity describing time dilation. The 100th episode had a free body diagram and several equations from Newtonian physics. I give the team a lot of respect on attention to detail. At this point, they could add Fermat’s Last Theorem as an Easter egg and I wouldn’t bat an eye.
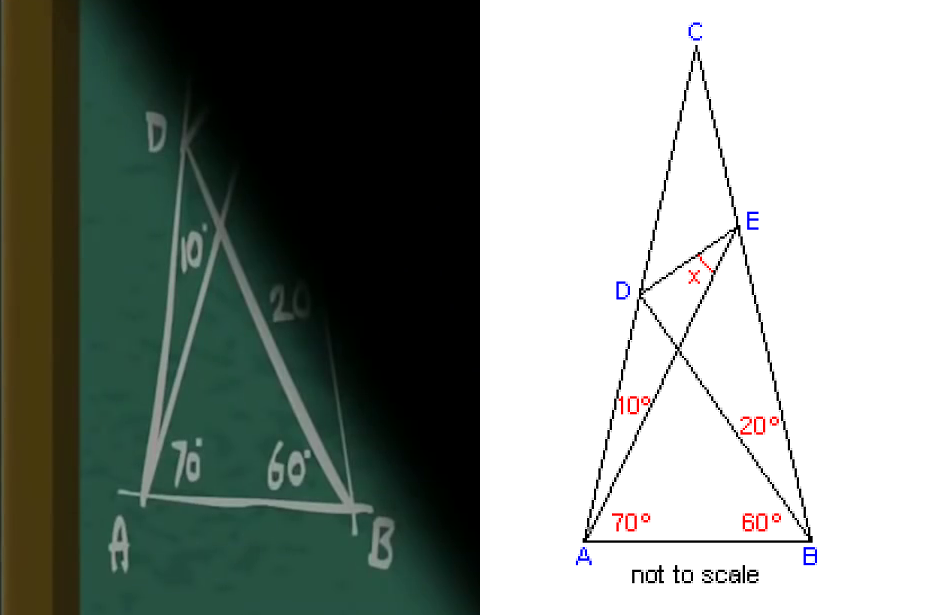
Let’s chase that assumption for a bit. It’s easiest to see the diagram at the start and end of the contest.
On a closer look, the diagram looked vaguely familiar. Let’s set that aside for now and ask what else we can figure out.
At the beginning, there’s no text accompanying the diagram, so the problem must require no additional detail. At the end, the writing on the chalkboard only involves lines, triangles, and angles. Notably, no trigonometry and no side lengths. If it is a real problem, then it’s an angle chasing problem. Yet for an angle chasing problem, this is a surprisingly long proof. In my experience, angle chasing is pretty short, but Sunset and Twilight have filled an entire chalkboard with derivations.
(Again, at this point it’s only likely this is a real proof. What I’m doing here is finding out what a real proof would imply to help narrow down what the problem is. Based on how easy/hard it is to find a problem matching those deductions, I can adjust how likely I believe the proof is real. It’s possible the animators made a new geometry problem just for this movie, but I don’t think they’re crazy enough to do that for 25 seconds of animation.)
After some searching, I found the World’s Hardest Easy Geometry Problem. It hits all the key details: it uses only angles, requires only basic geometry, and has a difficult solution. I had actually seen this problem several years ago, which explains why the problem looked so familiar. The solution is \(x = 20^\circ\), which matches the answer from the movie.
and the given angles match up
and \((180 - 80) / 2 = 50\) shows up in both proofs.
Jackpot.
Verification
It’s certain this is a real geometry problem and proof. The only question left is to see how accurate the animators were.
Unfortunately for geometry enthusiasts, the movie spends very little time on the proof. Most of the proof is in this montage.

Stepping through this frame by frame gives the money shot.
This is the clearest shot of the chalkboard in the entire sequence. It’s also only shown for 0.2 seconds. A lot of work, for something that people will barely notice. The text lines up exactly with the second section of the proof.
However, it’s not perfect. Neither character draws the parallel to \(AB\) through \(D\), so there’s no point \(F\). Also, neither character draws segment \(AF\), so there’s no point \(G\). They’re both pulling these points out of nowhere. (If curious, click here for the diagram with added lines.) Also, the derivation \(\angle CDF = \angle CAB = 70 + 10 = 80^\circ\) has a small animation error. They accidentally drew \(- 80^\circ\) instead of \(= 80^\circ\).
The rest of the montage has nothing new. There’s this shot
which is a closeup of the top line of the second section, and this shot
which is a closeup of the \(\angle DEF = 30 + x = (180 - 80)/2\) line.
The first section of the proof only appears in the final shot. I had to zoom to see it, so it’s a bit blurry.
It reads
\[\angle ACB = 180 - (10+70) - (60+20) = 20^\circ\] \[\angle AEB = 180 - 70 - (60+20) = 30^\circ\]which again lines up with
The ending of the proof is best seen in the two closeups
which gives the final lines
\[\triangle ACG \cong \triangle CAE\] \[FC - CE = FA - AG = \overline{FE} = \overline{FG}\] \[\overline{FG} = \overline{FD}, \overline{FE} = \overline{FD}\]There are some more errors here. Sunset derives \(\angle CDF = \angle CAB = 70+10 = 80^\circ\) after writing \(\overline{FE} = \overline{FG}\); she’s proving things out of order. There’s no way she can justify \(\overline{FC} - \overline{CE} = \overline{FA} - \overline{AG}\) before that line. (Points to Twilight for proving things in the right order. It could be a subtle way to show Twilight is better, but it’s probably an error.)
Going back to the original proof, both characters skipped stating triangles \(\triangle DFG\) and \(\triangle AGB\) are equilateral. However, that’s reasonable. They’ve shown the angles of \(\triangle DFG\) and \(\triangle AGB\) are all \(60^\circ\), so the equal side lengths are implied. They also skipped justifying \(\overline{FC} = \overline{FA}\) from isosceles \(\triangle FCA\), and didn’t prove \(CG\) is the angle bisector of \(\angle C\), but these are also reasonable skips given the diagram.
Overall, I’m impressed the animators got as much right as they did. It also shows that Sunset almost, almost solved the problem, since her only error is an arithmetic mistake at the end. Sometimes that’s how these things go. Now that I’ve done all of this, I actually like this scene more. Sunset Shimmer’s fall to villainy was based around a desire to be the best at all costs, and her redemption is about her anxiety at failing to make up for all the damage she caused. With all the self-loathing and setbacks she goes through, it’s easy to forget she’s almost as good as Twilight.
Nice job team! Now, if only you remembered how to spell…