Posts
-
Late Takes on OpenAI o1
CommentsI realize how late this is, but I didn’t get a post out while o1 was fresh, and still feel like writing one despite it being cold. (Also, OpenAI just announced they’re going to ship new stuff starting tomorrow so it’s now or never to say something.)
OpenAI o1 is a model release widely believed (but not confirmed) to be a post-trained version of GPT-4o. It is directly trained to spend more time generating and exploring long, internal chains of thought before responding.
Why would you do this? Some questions may fundamentally require more partial work or “thinking time” to arrive at the correct answer. This is considered especially true for domains like math, coding, and research. So, if you train a model to specifically use tokens for thinking, it may be able to reach a higher ceiling of performance, at the cost of taking longer to generate an answer.
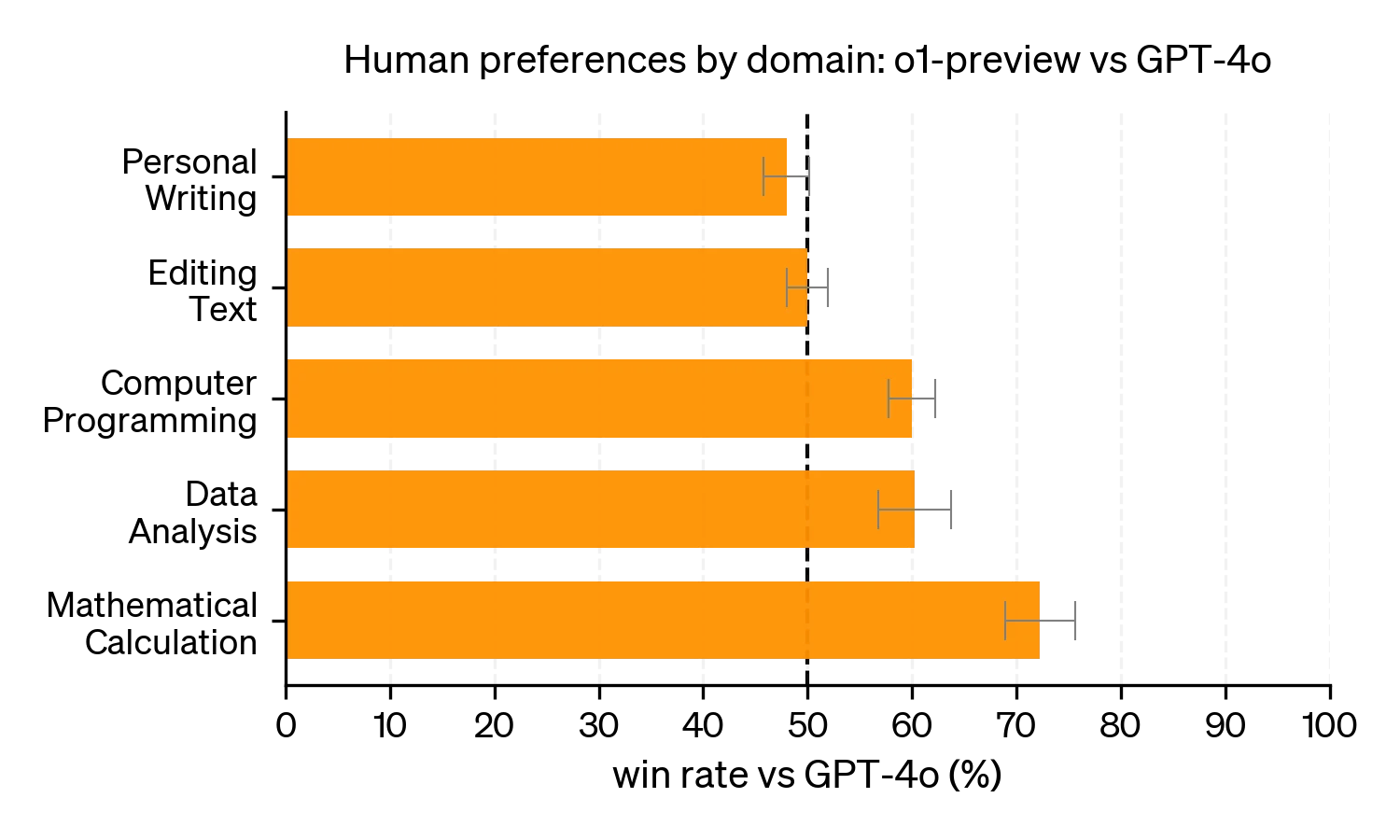
Based on the launch post and system card, this has been the case. o1 was not preferred over GPT-4o on simpler questions on editing text, but was more preferred on programming and math calculation questions.
The Compute View
When GPT-4 was first announced, OpenAI did not disclose how it was implemented. Over time, the broad consensus (from leaks and other places) is that GPT-4 was a mixture-of-experts model, mixing 8 copies of a 220B parameter model.
This was a bit disappointing. To quote George Hotz, “mixture[-of-experts] models are what you do when you run out of ideas”. A mixture of experts model is “supposed” to work. I say “supposed” in quotes, because things are never quite that easy in machine learning, but for some time mixture-of-experts models were viewed as a thing you used if you had too much compute and didn’t know what to do with it.
I think this view is a bit too simple. The Switch Transformers paper showed MoE models had different scaling properties and could be more compute efficient. But, broadly, I’d say this is true. If you think of compute as water filling a bowl, mixture models are a way to add a dimension to how you store water. The argument for them is that instead of building a bigger bowl, you should just use more bowls.
o1 feels similar to me. The analogy stops working here, but the dimension is the amount of compute you use at test-time - how many response tokens you generate for each user query. One way to describe o1 is that it may not be as good if you gave it the same 1-shot budget as a standard LLM, but it’s been trained to be better at spending larger compute budgets. So, as long as you commit to giving o1 more test-time compute, it can do better than just taking the best of N independent attempts from GPT-4o.
A shift towards more test-time compute increases the affordances of where compute can be allocated. In general, if you have many compounding factors that multiply each other’s effectiveness, then it’s best to spread attention among all of them rather than going all-in on one. So if you believe compute is the bottleneck of LLMs, you ought to be looking for these new dimensions where compute can be channeled, and push the compute along those channels.
Scaling Laws View
In May 2024, Noam Brown from OpenAI gave a talk at the University of Washington on the power of planning and search algorithms in AI, covering his work on expert-level systems playing Texas Hold’em and Diplomacy. Notably, most talks in the lecture series have their recordings uploaded within a few days. This one was not uploaded until September, after o1’s release. The current guess is that Noam or OpenAI asked and got a press embargo. If true, that makes this video especially useful for understanding OpenAI o1.
(It is uniquely dangerous to link an hour-long research talk in the middle of a blog post, because you may watch it instead of reading the post. It is good though. Do me a favor, watch it later?)
In this talk, Noam mentions an old paper on Scaling Laws in Board Games. This paper was from a hobbyist (Andy Jones), studying scaling laws in toy environments. I remember reading this paper when it came out, and I liked it. I then proceeded to not fully roll out the implications. Which I suppose is part of why I’m talking about o1 rather than building o1.
I think it’s really hard to put yourself in the mindset of - everything’s obvious in retrospect. But at the time, it was not obvious this would work so well.
(Noam on computer poker, and other planning-based methods.)
Among other results, the board games scaling law paper found a log-linear trade-off between train time compute and test time compute. To achieve a given fixed Elo target in the game of Hex, each 10x of train-time compute could be exchanged for 15x test-time compute. (Of course, the best model would use both.)
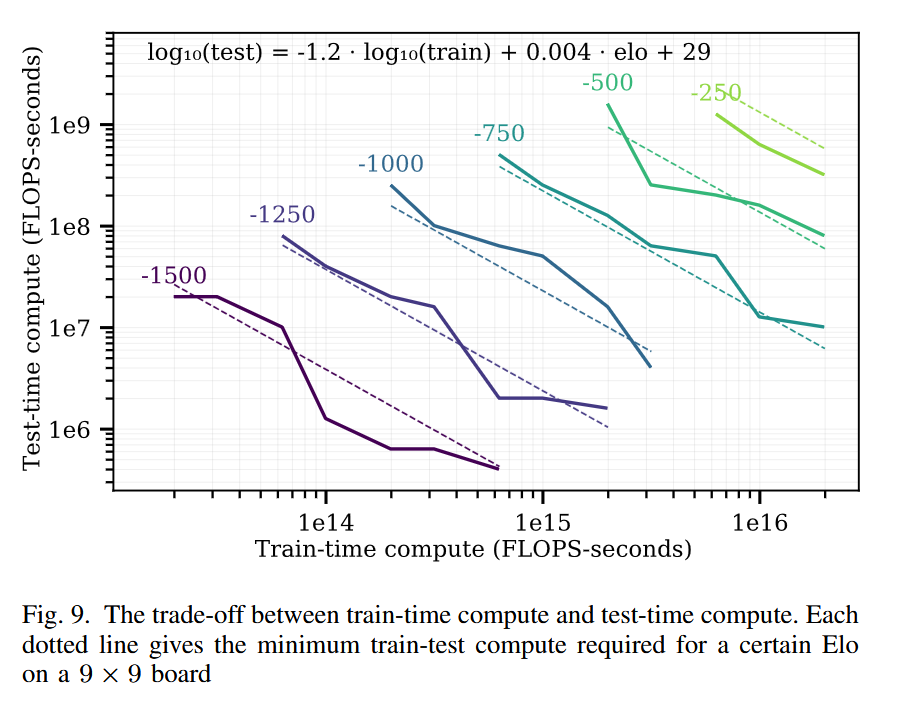
Nice chart, I’m a fan. Now let’s drop our science hat and think about money instead. Compute isn’t exactly linear in dollars (there are big fixed costs), but it’s approximately linear. So let’s replot one of these curves on a standard plot, no log-log scaling.
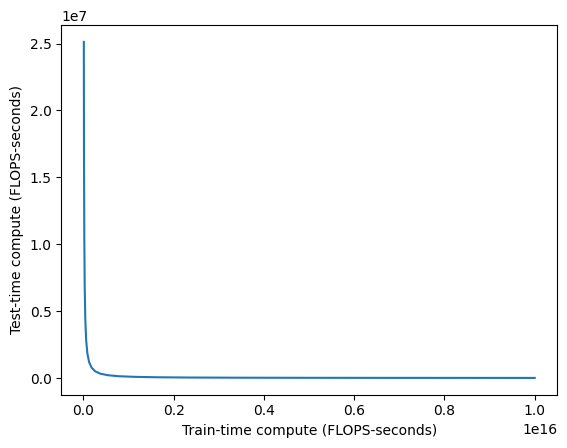
See, there’s a 10^8 difference between the two axes. It’s like asking for a million dollars in training when you could spend 1 more cent per inference call instead. It’s just so obviously worth it to do more test-time compute instead of pushing up a log curve.
The plot above is an ideal case, where you have a ground truth objective function. Two-player perfect information games have been known to be especially amenable to search for decades. Once you move to real, messier problems, the conversion factors are worse, I suspect by several orders of magnitude. But, in the face of something that’s literally millions of times cheaper…you should at least check how much worse it is for your use case, right?
Any researcher who believes in scaling but has not already poked at this after o1’s release is not a serious person.
User View
The paradigm of more test-time compute is new, but is it good? Do people actually need what o1 provides?
I read through a recent AMA with OpenAI executives on r/ChatGPT, and it struck me how much people didn’t really ask about benchmarks. Most questions were about context windows, better image support, opening access to Sora, and more. I have no firsthand experience with Character.AI models, but my vague impression was that a lot of their users are similar. They don’t need their AI characters to have a ton of reasoning power, or ability to do research across many disciplines. They just want good roleplay, coherence across time, and conversational abilities.
Only weirdos care about how smart the models are. Most people just want new features and nicer UX.
This is very reductive, because a lot of features come from how smart the models are, but I feel it’s still an important perspective. When LLMs first entered public consciousness, one big selling point was how fast they generated text that a human would have trouble generating. People marveled at essays and code written in seconds, when both writing and coding are typically hard. Attention spans tend to only go down. Creating a paradigm where you ask users to wait longer is certainly a bold choice.
That said, it’s not that much slower. Inference has come a long way since 2023, and I think people will normalize to the longer response times if they have questions that are at the frontier of model capabilities. I’m personally pretty bad at leveraging LLMs for productivity (my mental model for what questions are worth asking is about 6 months out of date), so I’m often not at the frontier and asking questions that could have been answered by weaker and faster models.
This ties into a concept from Dario’s Machines of Loving Grace essay: that as AI becomes better, we need to think in terms of marginal returns on intelligence. AI labs are incentivized to find domains where the marginal returns are high. I think those domains exist (research comes to mind), but there’s plenty of domains where the marginal returns flatten out pretty quick!
Safety View
I work on an AI safety team now. That makes me feel slightly more qualified to speculate on the safety implications.
One of the early discussion points about LLMs was that they were easier to align than people thought they’d be. The way they act is somewhat alien, but not as alien as they could be.
We seem to have been given lots of gifts relative to what we expected earlier: for example, it seems like creating AGI will require huge amounts of compute and thus the world will know who is working on it, it seems like the original conception of hyper-evolved RL agents competing with each other and evolving intelligence in a way we can’t really observe is less likely than it originally seemed, almost no one predicted we’d make this much progress on pre-trained language models that can learn from the collective preferences and output of humanity, etc.
(Footnote from Planning for AGI and Beyond, Feb 2023)
Alignment is not solved (that’s why I’m working on safety), but some things have been surprisingly fine. Let’s extend this “gifts” line of thought. Say you magically had two systems, both at AGI level, with equal capability, trained in two ways:
- A system primarily using supervised learning, then smeared with some RL at the end.
- A system with a small amount of supervised learning, then large fractions of RL and search afterward.
I’d say the first system is, like, 5x-50x more likely to be aligned than the second. (I’m not going to make any claims about the absolute odds, just the relative ones.) For this post I only need a narrower version of that claim: that the first system is much more likely to be supervisable than the second. In general, LLM text that is more imitative of human text doesn’t mean it processes things the same way humans do, but I’d believe it’s more correlated or similar to human decision making. See “The Case for CoT Unfaithfulness is Overstated” for further thoughts on this line. Chain-of-thoughts can be fake, but right now they’re not too fake.
In contrast, if your system is mostly RL based, then, man, who knows. You are putting a lot of faith into the sturdiness of your reward function and your data fully specifying your intentions. (Yes I know DPO-style implicit reward functions are a thing, I don’t think they change the difficulty of the problem.) In my mind, the reason a lot of RLHF has worked is because the KL regularization to a supervised learning baseline is really effective at keeping things on rails, and so far we’ve only needed to guide LLMs in shallow ways. I broadly agree with the Andrej Karpathy rant that RLHF is barely RL.
So, although o1 is exciting, I find it exciting in a slightly worrying way. This was exacerbated after anecdotal reports of weird tokens appearing in the summarized chain-of-thought, stuff like random pivots into Chinese or Sanskrit.

It was all reminiscent of an old AI scare. In 2017, a group from Facebook AI Research published a paper on end-to-end negotiation dialogues. (Research blog post here.) To study this, they used an item division task. There is a pool of items, to be divided between the two agents. Each agent has a different, hidden value function on the items. They need to negotiate using natural language to agree on a division of the items. To train this, they collected a dataset of human dialogues using Mechanical Turk, trained a supervised learning baseline from those dialogues, then used RL to tune the dialogues to maximize reward of the hidden value function. A remarkably 2024-style paper, written 7 years ago. Never let anyone tell you language-agents are a new idea.
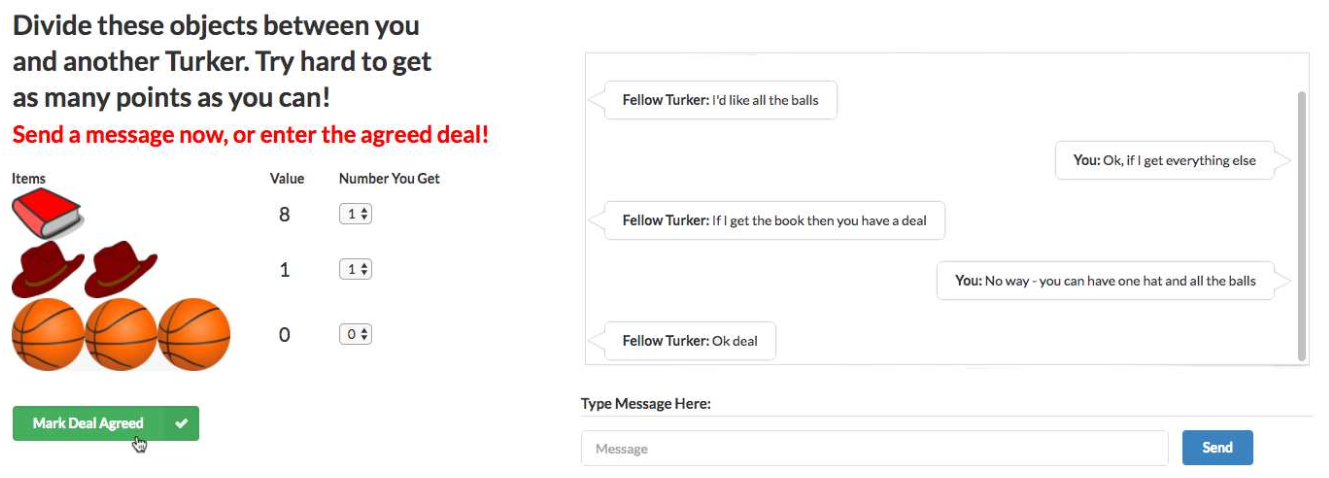
Unfortunately no one remembers this paper for being ahead of its time. As part of the paper, the authors noted found that letting the agents do RL against each other too much would devolve into garbage text.
This made sense: nothing about the reward function encouraged maintaining human readable text. Adversarial setups were notoriously brittle, adding RL made it worse. Diverging from human readability was a very predictable outcome. The authors stopped that run and switched to a less aggressive RL strategy.
We gave some AI systems a goal to achieve, which required them to communicate with each other. While they were initially trained to communicate in English, in some initial experiments we only reward them for achieving their goal, not for using good English. This meant that after thousands of conversations with each other, they started using words in ways that people wouldn’t. In some sense, they had a simple language that they could use to communicate with each other, but was hard for people to understand. This was not important or particularly surprising, and in future experiments we used some established techniques to reward them for using English correctly.
(Mike Lewis, lead author of the paper)
Pop science news outlets ran the story as “Facebook’s AI robots shut down after they start talking to each other in their own language” and it spread from newspaper to newspaper like wildfire.

(One of many, many headlines.)
It got so bad that there are multiple counter-articles debunking it, including one from Snopes. The whole story was very laughable and silly then, and was mostly a lesson in what stories go viral rather than anything else.
I feel it’s less silly when o1 does it. Because o1 is a significantly more powerful model, with a much stronger natural language bias, presumably not trained adversarially. So where are these weird codeword-style tokens coming from? What’s pushing the RL to not use natural language?
You can tell the RL is done properly when the models cease to speak English in their chain of thought
One theory of language is that its structure is driven by the limitations of our communication channels. I was first introduced to this by (Resnick and Gupta et al 2020), but the idea is pretty old.
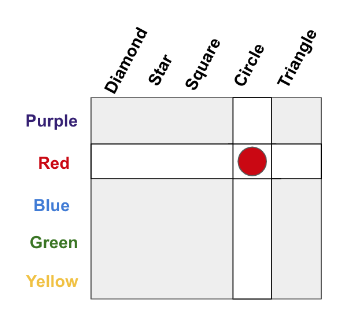
In this example, suppose you wanted to communicate a specific object, like “red circle”. There are two constraints: how much memory you have for concepts, and how much bandwidth you have to communicate a message. One choice is to ignore the structure, treat every object as disconnected, and store 25 different concepts. For the sake of an example, let’s say those concepts map to letters A, B, C, D, …, Y. To communicate an object, you only need to use 1 letter.
What if we can’t remember 25 things? We can alternatively remember 10 concepts: 5 for the colors, and 5 for the shapes. Let’s say colors are A, B, C, D, E and shapes are 1, 2, 3, 4, 5. Now our memory requirements are lower, we only need to know 10 things. But our communication needs to specify an object are higher. We have to 2 pieces, a letter and a number. There’s the fundamental tradeoff between memory and bandwidth.
o1 is incentivized to get all its thinking done within the thinking budget. That means compressing information into fewer tokens. The speculation (again, this is speculation) is that the RL is doing its job properly, responding to the pressure for conciseness, and that occasionally causes encoding of information into strings outside human readability. Which isn’t great for auditing or supervision!
RL and search are uniquely awful at learning the wrong goal, or finding holes in evaluation functions. They are necessary tools, but the tools have sharp edges. They are powerful because you can give them anything, and they’re tricky because they’ll give you anything back.
In this LLM-driven age, we have so far lived with models that are surprisingly amenable to interpretation. I think it’s possible this is because we’ve only done these barely-RL versions of RLHF. So now, with things trending towards actual RL, maybe we’ll lose that. Maybe we lose these “gifts” we observed in the first versions of ChatGPT. That would suck a lot!
It is too early to declare that will come to pass. But o1 made me feel more likely it could. As the field pursues better autonomy and AI agents, I’d appreciate if people remembered that methods used for benchmark chasing are not alignment-agnostic. On any axis, you can be positive or negative, but it’s really hard to land on exactly zero. Declaring the answer is zero is usually just a shorthand of saying you don’t want to spend effort on figuring out the direction. That’s a totally valid choice! In other contexts, I make it all the time. I just think that when it comes to alignment, it’d be nice if people thought about whether their work would make alignment harder or easier ahead of time. If your plan is to let the AI safety teams handle it, please be considerate when you make our lives harder.
-
Nine Years Later
CommentsSorta Insightful turns nine years old today!
Highlights
I took a break from writing puzzles this year. That’s led to a lot more free time. Puzzle writing has been one of my main recent hobbies, but I’ve found the problem is that I can’t do low key puzzlehunt writing. I either go all-in or I don’t, and when I go all-in, it takes up enough headspace that I have trouble making any other major life decisions. This year was a year where I needed to do other things. I wanted to change things up.
And I did change things up! Some of it was silent backend migrations (both Universal Analytics and my time tracker got deprecated this year), but the most notable change is that I switched career trajectories to AI safety.
I try to keep my Twitter / X usage low, but I retweet all posts whenever I write them, and I’ve noticed my switch into AI safety post has had significantly more Twitter engagement than my other posts. I chalk this up to “the alignment mafia” - a distributed set of people who reshare and promote anything supporting their views on AGI. Listen, I appreciate the support, but I haven’t done anything yet! Chill.
The time it took me to navigate my career change was much less than the time I’ve spent on puzzle writing in the past. I expected to fill that void with more blog writing, but that’s not what happened. So, what filled the void in its place?
Video games. It was video games. A quick review of some of them:
Hi-Fi Rush
Hi-Fi Rush starts simple but gets great once you unlock all the battle mechanics and get into the rhythm based flow. It’s very colorful, never takes itself that seriously, and is filled with fantastic set pieces.
Islands of Insight
Islands of Insight is…fine? It pitched itself as a puzzle-based MMO, where the highlight is a huge set of handmade Nikoli-style logic puzzles in an explorable world. The puzzles are good, but the game is poorly optimized, the social MMO aspects are pretty minimal, and the huge skill tree and unlockables feel like they’re just there to encourage higher engagement, rather than being more fun. The puzzles are great though, and if that’s good enough for you, I had fun with that.
Undertale Yellow
Undertale Yellow is a fantastic fan game, that’s been in development for 7 years and comes out feeling like a canon entry made by Toby Fox. I have small nitpicks about the plot and lack of variety in pacifist boss strategies, but the overall package works. I would have gladly paid money for this, but it’s free. If you liked Undertale check it out.
Hades 1
I bought the first Hades three years ago and never installed it. When Hades 2 went into early access, it was a great excuse to play the first one. I pushed up to Epilogue, all weapon aspects, and 21 heat before setting it down. At some point, it does get easy to fall into the builds you know are overpowered, but that’s the fate of every roguelike. What Hades 1 does well is make you feel overpowered when you get a good run going - and then killing you regardless if you don’t respect the bosses enough. It just does a lot of things right. I don’t like how grindy the story progression gets by the end, where you’re just waiting for a character to provide a dialogue option, but most players will not reach that point.
Incremental Games
Incremental games were a mistake, do not recommend. If you’re unfamiliar with the genre, Cookie Clicker is the prototypical example. You start with a small number of resources, then achieve exponentially larger resources through increasingly complicated progression and automation systems. I tried one of the highly recommended ones, and no joke, it took up 4 months of my life. If you are the kind of person who likes theorycrafting stat builds to maximize damage throughput, incremental games are a game where you only do that. Except, instead of maximizing damage, you’re minimizing time-to-unlock the next progression layer. I was spending 3 hours a day to push my game to a state where I could minimize how much time I’d need to wait to unlock the next layer, and if I didn’t spend those 3 hours I would have had to wait days for progress instead. It felt a lot like machine learning work, where you try to get everything done so that you can let the model train overnight and inspect it next morning. The experience was interesting, but I wouldn’t go through it again.
Statistics
Posts
I wrote 9 posts this year, up from 6 last year.
Time Spent
I spent 139 hours, 56 minutes writing for my blog this year, around 0.75x as much as last year.
View Counts
These are view counts from August 18, 2023 to today.
300 2023-08-18-eight-years.markdown 247 2023-09-05-efnw-2023.markdown 628 2023-11-25-neopoints-making-guide.markdown 15837 2024-01-11-ai-timelines-2024.markdown 1939 2024-01-21-mh-2024.markdown 5076 2024-03-23-crew-battle.markdown 826 2024-04-30-puzzlehunting-201.markdown 8641 2024-07-08-tragedies-of-reality.markdown 3923 2024-08-06-switching-to-ai-safety.markdownThis continues to be a reminder that my view counts are heavily driven by who reshares things. I expected the AI related posts to be popular, but the post on the math of Smash Bros. crew battles is a big outlier. I shared it to the Smash subreddit, someone from there shared it to Hacker News, and that’s why it has so many views. (By the way, I’ve made some minor edits since that post went live, including a proof sketch for the final conjecture. Check it out if you missed it.)
Based on Twitter views, I can also see there’s a 6% clickthrough rate from my tweet saying I was joining an AI safety team to people actually reading the blog post.
Posts in Limbo
Is this a good time to confess that I never look back at the list of in-progress posts I write each year? I just write up the list, never read it, then go “oh yeah, that” when I reread my old posts to prepare the next anniversary post.
I’m no longer sure I get any value from sharing half-baked ideas, and may cut this in the future.
Post about Dominion:
Odds of writing this year: 5%
Odds of writing eventually: 10%I haven’t touched my draft of this in a long, long time. I’m realizing it’s the kind of thing that could form a good Youtube essay (big fan of the History of the 2002-2005 Yu-Gi-Oh! meta video), but longform video content is not my skillset and not something I’m interested in getting better at.
Post about Dustforce:
Odds of writing this year: 20%
Odds of writing eventually: 60%One hypothesis of the world is that positive and negative reinforcement plays a much larger role in behavior than people think it does. I’m partial to this, because I can tell I’ve played less Dustforce recently, almost entirely because of my personal laptop developing sticky key issues that make it just a bit more annoying to play. The game is still great, but it’s not a game you want to play with a keyboard that eats 5% of your jumps at random. This also affected my blogging motivation. Imagine trying to write longform text when your E key randomly sends 0 E presses or 2 E presses each time you touch it. So far, blogging has been saved by either writing on my work laptop or plugging in an external keyboard. Neither of those solutions work for Dustforce, since I won’t install it on my work laptop, and my external keyboards have key ghosting issues.
My personal laptop is getting pretty worn down, and I’m going to need to replace it before I travel for Mystery Hunt this year. (Pro tip: gaming laptops tend to prioritize good initial specs over long-term reliability.) One more thing to change - those video games aren’t gonna play themselves.
-
I'm Switching Into AI Safety
CommentsYou can read the title. As of last month, I’ve been winding down my existing robotics projects, and have switched to the AI safety team within Google DeepMind. Surprise!
It took me a while to start working on this post, because my feelings on AI safety are complicated, but changing jobs is a big enough life update that I have to write this post. Such is the life of a blogger.
The Boring Personal Reasons
I’ve been working on the robotics team for 8 years now, and I just felt like I needed to mix it up. It was a little unsettling to realize I had quietly become one of the most senior members of the team, and that I had been there longer than my manager, my manager before that, and my manager before that. Really, this is something I thought about doing three years ago, but then my puzzlehunt team won MIT Mystery Hunt, meaning we had to write next year’s Mystery Hunt. Writing Mystery Hunt took up all of my 2022, and recovering from it took up much of my 2023. (That and Tears of the Kingdom, but let’s not talk about that.)
Why change fields, rather than change within robotics? Part of me is just curious to see if I can. I’ve always found the SMBC “Seven Years” comic inspiring, albeit a bit preachy.

(Edited from original comic)
I believe I have enough of a safety net to be okay if I bomb out.
When discussing careers with someone else, he said the reason he wasn’t switching out of robotics was because capitalism rewards specialization, research especially so. Robotics was specialized enough to give him comparative advantages over more general ML. That line of argument makes sense, and it did push against leaving robotics. However, as I’ve argued in my previous post, I expect non-robotics fields to start facing robotics-style challenges, and believe that part of my experience will transfer over. I’m also not starting completely from zero. I’ve been following AI safety for a while. My goal is to work on projects that can leverage my past expertise, while I get caught up.
The Spicier Research Interests Reasons
The current way robot agents are trained can broadly be grouped into control theory, imitation learning, and reinforcement learning. Of those, I am a fan of reinforcement learning the most, due to its generality and potential to exceed human ability.
Exceeding human ability is not the current bottleneck of robot learning.
Reinforcement learning was originally a dominant paradigm in robot learning research, since it led to the highest success rates. Over the years, most of its lunch has been eaten by imitation learning methods that are easier to debug and show signs of life earlier. I don’t hate imitation learning, I’ve happily worked on several imitation learning projects, it’s just not the thing I’m most interested in. Meanwhile, there are some interesting applications of RL-style ideas to LLMs right now, from its use in RLHF to training value functions for search-based methods like AlphaProof.
When I started machine learning research, it was because I found learning and guiding agent behavior to be really interesting. The work I did was in a robotics lab, but I always cared more about the agents than the robots, the software more than the hardware. What kept me in robotics despite this was that in robotics, you cannot cheat the real world. It’s gotta work on the real hardware. This really focused research onto things that actually had real world impact, rather than impact in a benchmark too artificial to be useful. (Please, someone make more progress on reset-free RL.)
Over the past few years, software-only agents have started appearing on the horizon. This became an important decision point for me - where will the real-world agents arrive first? Game playing AIs have been around forever, but games aren’t real. These LLM driven systems…those were more real. In any world where general robot agents are created, software-only agents will have started working before then. I saw a future where more of my time was spent learning the characteristics of the software-hardware boundary, rather than improving the higher-level reasoning of the agent, and decided I’d rather work on the latter. If multimodal LLMs are going to start having agentic behaviors, moving away from hardware would have several quality of life benefits.
One view (from Ilya Sutskever, secondhand relayed by Eric Jang) is that “All Successful Tech Companies Will be AGI Companies”. It’s provocative, but if LLMs are coming to eat low-level knowledge work, the valuable work will be in deep domain expertise, to give feedback on whether our domain-specific datasets have the right information and whether the AI’s outputs are good. If I’m serious about switching, I should do so when it’s early, because it’ll take time to build expertise back up. The right time to have max impact is always earlier than the general public thinks it is.
And, well, I shouldn’t need to talk about impact to justify why I’m doing this. I’m not sitting here crunching the numbers of my expected utility. “How do we create agents that choose good actions” is just a problem I’m really interested in.

(I tried to get an LLM to make this for me and it failed. Surely this is possible with the right prompt, but it’s not worth the time I’d spend debugging it.)
The Full Spice “Why Safety” Reasons
Hm, okay, where do I start.
There’s often a conflation between the research field of AI safety and the community of AI safety. It is common for people to say they are attacking the field when they are actually attacking the community. The two are not the same, but are linked enough that it’s not totally unreasonable to conflate them. Let’s tackle the community first.
I find interacting with the AI safety community to be worthwhile, in moderation. It’s a thing I like wading into, but not diving into. I don’t have a LessWrong account but have read posts sent to me from LessWrong. I don’t read Scott Alexander but have read a few essays he’s written. I don’t have much interaction with the AI Alignment Forum, but have been reading more of it recently. I don’t go to much of the Bay Area rationalist / effective altruism / accelerationist / tech bro / whatever scene, but I have been to some of it, mostly because of connections I made in my effective altruism phase around 2015-2018. At the time, I saw it as a movement I wasn’t part of, but which I wanted to support. Now I see it as a movement that I know exists, where I don’t feel much affinity towards it or hatred against it. “EA has problems” is a statement I think even EAs would agree with, and “Bay Area rationalism has problems” is something rationalists would agree with too.
The reason AI safety the research topic is linked to that scene is because a lot of writing about the risks of AGI and superintelligence originate from those rationalist and effective altruist spaces. Approving of one can be seen as approving the other. I don’t like that I have to spill this much digital ink spelling it out, but that is not the case here. Me thinking AI safety is important is not an endorsement for or against anything else in the broader meme space it came from.
Is that clear? I hope so. Let’s get to the other half. Why do I think safety is worth working on?
* * *
The core tenets of my views on AI safety are that:
- It is easy to have an objective that is not the same as the one your system is optimizing, either because it is easier to optimize a proxy objective (negative log likelihood vs 0-1 classification accuracy), or because your objective is hard to describe. People run into this all the time.
- It’s easy to have a system that generalizes poorly because you weren’t aware of some edge case of its behavior, due to insufficient eval coverage, poor model probing, not asking the right questions, or more. This can either be because the system doesn’t know how to handle a weird input, or because your data is not sufficient to define the intended solution.
- The way people solve this right now is to just…pay close attention to what the model’s doing, use humans in the loop to inspect eval metrics, try small examples, reason about how trustworthy the eval metrics are, etc.
- I’m not sold our current tooling scales to better systems, especially superhuman systems that are hard to judge, or high volume systems spewing millions of reviewable items per second.
- I’m not sold that superhuman systems will do the right thing without better supervision than we can currently provide.
- I expect superhuman AI in my lifetime.
- The nearest-term outcomes rely on the current paradigm making it to superhuman AI. There’s a low chance the current paradigm gets all the way there. The chance is still higher than I’m comfortable with.
In so far as intelligence can be defined as the ability to notice patterns, pull together disparate pieces of information, and overall have the ability to get shit done, there is definitely room to be better than people. Evolution promotes things that are better at propagating or replicating, but it works slow. The species that took over the planet (us) is likely the least intelligent organism possible that can still create modern civilization. There’s room above us for sure.
I then further believe in the instrumental convergence theory: that systems can evolve tendencies to stay alive even if that is not directly what their loss function promotes. You need a really strong optimizer and model for that to arise, so far models do not have that level of awareness, but I don’t see a reason that wouldn’t happen. At one point, I sat down and went through a list of questions for a “P(doom)” estimate - the odds you think AI will wreck everything. How likely do you think transformative AI is by this date, if it exists how likely is it to develop goal-seeking behavior, if it has goals how likely are they to be power-seeking, if it’s power-seeking how likely is it to be successful, and so on. I ended up with around 2%. I am the kind of person who thinks 2% risks of doom are worth looking at.
Anecdotally, my AI timelines are faster than the general public, and slower than the people directly working on frontier LLMs. People have told me “10% chance in 5 years” is crazy, in both directions! There is a chance that alignment problems are overblown, existing common sense in LLMs will scale up, models will generalize intent correctly, and OSHA / FDA style regulations on deployment will capture the rare mistakes that do happen. This doesn’t seem that likely to me. There are scenarios where you want to allow some rule bending for the sake of innovation, but to me AI is a special enough technology that I’m hesitant to support a full YOLO “write the regulations if we spill too much blood” strategy.
I also don’t think we have to get all the way to AGI for AI to be transformative. This is due to an argument made by Holden Karnofsky, that if a lab has the resources to train an AI, it has the resources to run millions of copies of that AI at inference time, enough to beat humans due to scale and ease of use rather than effectiveness. (His post claims “several hundred millions of copies” - I think this is an overestimate, but the core thesis is correct.)
So far, a number of alignment problems have been solved by capitalism. Companies need their AIs to follow user preferences enough for their customers to use them. I used to have the view that the best thing for alignment would be getting AI products into customer’s hands in low stakes scenarios, to get more data in regimes where no mistake was too dangerous. This happened with ChatGPT, and as I’ve watched the space evolve, I…wish there was more safety research than there has been. Capitalism is great at solving the blockers to profitability, but it’s also very willing to identify economic niches where you can be profitable while ignoring the hard problems. People are too hungry for the best models to do due diligence. The level of paranoia I want people to have about LLMs is not the level of paranoia the market has.
Historically, AI safety work did not appeal to me because of how theoretical it was. This would have been in the early 2010s, but it was very complexity theory based. Bounded Turing machines, the AIXI formulation, Nash equilibria, trying to formalize agents that can take actions to expand their action space, and so on. That stuff is my jam, but I was quite pessimistic any of it would matter. I would like someone to be trying the theory angle, but that someone isn’t me. There is now a lot of non-theory work going on in AI safety, which better fits my skill set. You can argue whether that work is actually making progress on aligning superhuman systems, but I think it is. I considered Fairness in Machine Learning too, but a lot of existing literature focuses on fairness in classification problems, like algorithmic bias in recidivism predictors and bank loan models. Important work, but it didn’t have enough actions, RL, or agent-like things to appeal to me. The claims of a war between the fairness and alignment communities feel overblown to me. The average person I’ve met from either is not interested in trying to make a person “switch sides”. They’re just happy someone’s joining to make the field larger, because there is so much work to do, and people have natural inclinations towards one or another. Even if the sociologies of the fields are quite different, the fundamentals of both are that sometimes, optimization goes wrong.
I’m aware of the arguments that most AI safety work so far has either been useless or not that different from broader AI work. Scaling laws came from safety-motivated people and are the core of current frontier models. RLHF developments led to InstructGPT, then ChatGPT. Better evaluation datasets to benchmark models led to faster hill climbing of models without corresponding safety guarantees. Most recently, there’s been hype about representation engineering, an interpretability method that’s been adopted enthusiastically…by the open-source community, because it enables better jailbreaks at cheaper cost. Those who don’t think safety matters brands this as typical Silicon Valley grandstanding, where people pretend they’re not trying to make money. Those who care about safety a lot call this safetywashing, the stapling of “safety” to work that does not advance safety. But…look, you can claim people are insincere and confused about anything. It is a nuclear weapon of an argument, because you can’t convince people it’s wrong in the moment, you just continue to call them insincere or confused. It can only be judged by the actions you take afterwards. I don’t know, I think most people I talk about safety with are either genuine, or confused rather than insincere. Aiming for safety while confused is better than not aiming at all.
So, that’s what I’m doing. Aiming for safety. It may not be a permanent move, but it feels right based on the current climate. The climate may turn to AI winter, and if it does I will reconsider. Right now, it is very sunny. I’d like it if we didn’t get burned.