The Blogging Gauntlet: May 10 - Splitwise is NP-Complete

This is part of The Blogging Gauntlet of May 2016, where I try to write 500 words every day. See the May 1st post for full details.

Say you go on a group trip. People foot the bill for different expenses, and need to get paid back later. Splitwise is a webapp that does all the bookkeeping for you.

As an example, consider this case. Alice, Bob, Carol, and Dave went on a trip together. Alice spent $60 and needs to get paid back by Bob, Carol, and Dave. Carol spent $20 and needs to get paid back by Bob and Dave. Dave spent $30 and needs to get paid back by Alice and Bob, and Alice’s share should be twice as big as Bob’s.

We can interpret these payments as a weighted directed graph, where people are vertices and edges are payments.

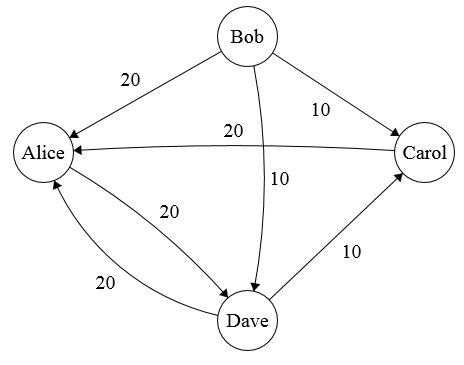
First payment graph

Alice needs $20 from everyone else, Carol needs $10 from Bob and Dave, and Dave needs $20 from Alice and $10 from Bob.

There are some redundancies in the graph. For example, Alice and Dave each need to pay each other $20. Since the net money between them is $0, we should just remove those edges to avoid doing extra transactions.

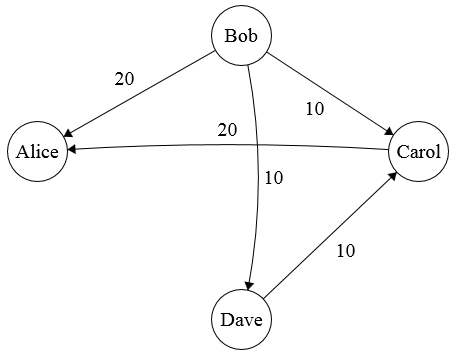
Second payment graph

Splitwise does this for you. In fact, it goes one step further. Splitwise tries to minimize the total number of transactions in the graph.

Let’s go back to the example above. Carol receives $20 in total from Bob and Dave, then pays $20 to Alice. Instead of routing their money through Carol to Alice, Bob and Dave could pay Alice directly. Carol is still net +$0 and Alice is still net +$20, but now Carol doesn’t have to pay anyone. That reduces the graph to this one.

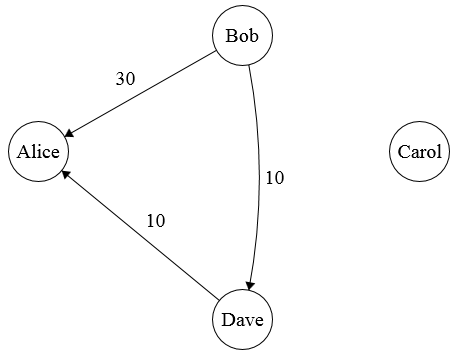
Third payment graph

Bob is sending $10 to Dave, who is sending $10 to Alice. We can simplify this by having Bob send $10 to Alice straight.

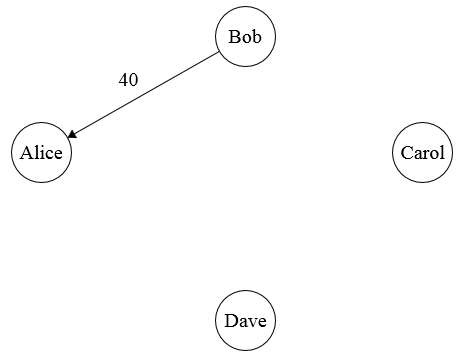
4th payment graph

We’ve simplified the graph down to a single payment. Pretty neat, right? You can see how a tool that does this automatically could be useful.

This raises an interesting question. How would you solve the Splitwise problem in general? We formalize the problem below.

Let $G = (V,E)$ be a weighted directed graph. Given $G$, construct an equivalent graph $G'$ such that every vertex $v$ receives/gives the same amount of money it would in $G$, and $G'$ has as few edges as possible.

Flow Representation

My first intuition was that the Splitwise problem was very similar to a network flow problem. You want to shuffle money around a graph while minimizing costs.

This motivated looking at the min-cost flow problem. In the min-cost flow problem, sending one unit of flow through an edge $(u,v)$ has some cost. We want to minimize cost while sending enough flow through the graph.

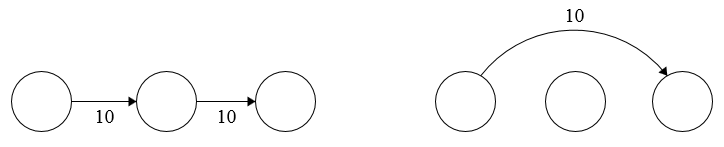
5th payment graph

The system on the left has $20$ total flow, while the system on the right has $10$ total flow. Assuming all edges have the same cost per unit flow, the latter graph is cheaper.

Min-cost flow is solvable through linear programming, but it’s not obvious that minimizing the flow in the graph is the same as minimizing the number of edges needed. So, I started looking elsewhere.

A Greedy Algorithm

Note that in flow problems, we assume only edges $(u,v)$ in the graph can send things to each other. In the Splitwise problem, anyone can send money to anybody else.

Instead of trying to reduce existing edges, let’s figure out how much everybody should pay, then add edges by ourselves. To minimize the number of edges, one natural idea is to send as much money as possible in every edge. This motivates the following algorithm.

Read the input $(V, E)$ to compute the net balance for everyone.
While someone owes money to somebody else:
Find the person $v_{max}$ who owes the most money.
Find the person $v_{min}$ who requests the most money.
Have $v_{max}$ send as much money as possible to $v_{min}$.
Update everyone’s net balance.

Here’s an example run. $v_1,v_2,v_3,v_4$ owe $1,$2,$3,$4 respectively, and $v_5,v_6$ request $5 each. The outputted set of edges is

$v_4$ sends $4 to $v_5$
$v_3$ sends $3 to $v_6$. (Before this step, $v_5$ is owed $1 and $v_6$ is owed $5.)
$v_2$ sends $2 to $v_6$. (Before this step, $v_5$ is owed $1 and $v_6$ is owed $2.)
$v_1$ sends $1 to $v_5$.

Every party that owes money must send money at least once, which gives a lower bound of $4$ transactions. This solution uses $4$ transactions, so it’s optimal.

On mentioning this problem to a friend, he pointed out the following example. Have $v_1,v_2$ owe $3, and $v_3$ owe $5. Then have $v_4$ request $6 and $v_5$ request $5. The output is

$v_3$ sends $5 to $v_4$
$v_2$ sends $3 to $v_5$
$v_1$ sends $2 to $v_5$
$v_1$ sends $1 to $v_4$

However, we only need $3$ transactions if $v_3$ sends money to $v_5$ in the first step.

He then proved Splitwise is NP-Complete, by showing Partition reduces to Splitwise.

NP-Completeness Proof

First, reformulate Splitwise as a decision problem.

Let $G = (V,E)$ be a weighted directed graph. Given $G$ and $k$, return whether there exists an equivalent graph $G'$ with at most $k$ edges.

Given a $G'$, we can verify it’s valid and has at most $k$ edges in polynomial time. So Splitwise is in NP.

Next, construct a reduction from Partition to Splitwise. Given a list $S$ of positive integers, we want to know if there is a partition $S_1,S_2$ such that both sets have the same total sum.

Given $S = \{a_1,a_2, \ldots, a_n\}$, construct $G$ with $n+2$ vertices $v_1,v_2,\ldots, v_{n+2}$. Add edges such that $v_i$ owes $a_i$, and $v_{n+1}, v_{n+2}$ request $\frac{1}{2}\sum_{i=1}^n a_i$ each.

Any solution to this instance must have at least $n$ transactions, because $n$ people owe money. Furthermore, if the solution has exactly $n$ transactions, $v_i$ must send $a_i$ for their transaction. The edges entering $v_{n+1}$ and $v_{n+2}$ correspond exactly to a partition of $\{a_1,\ldots,a_n\}$ Thus, there is a solution with $n$ transactions if and only if a partition exists. Since Partition is NP-Complete, it follows that Splitwise is NP-Complete. $\blacksquare$

Splitwise in Practice

It turns out the greedy algorithm gets pretty close to the optimal value in most cases. Based on a Quora post by a Splitwise founder, the site uses something similar.

So, Splitwise isn’t finding optimal solutions on a regular basis. Oh well. I still think it’s neat that an NP-Complete problem fell out at all.